BM算法

Posted on | In | | Visitors:
Words count in article: 2.4k

转自这里

1. BM（Boyer-Moore）算法

  • 思想：有模式串中不存在的字符，那么肯定不匹配，往后多移动几位，提高效率
    在这里插入图片描述
  • BM原理：坏字符规则，好后缀规则

1.1 坏字符规则

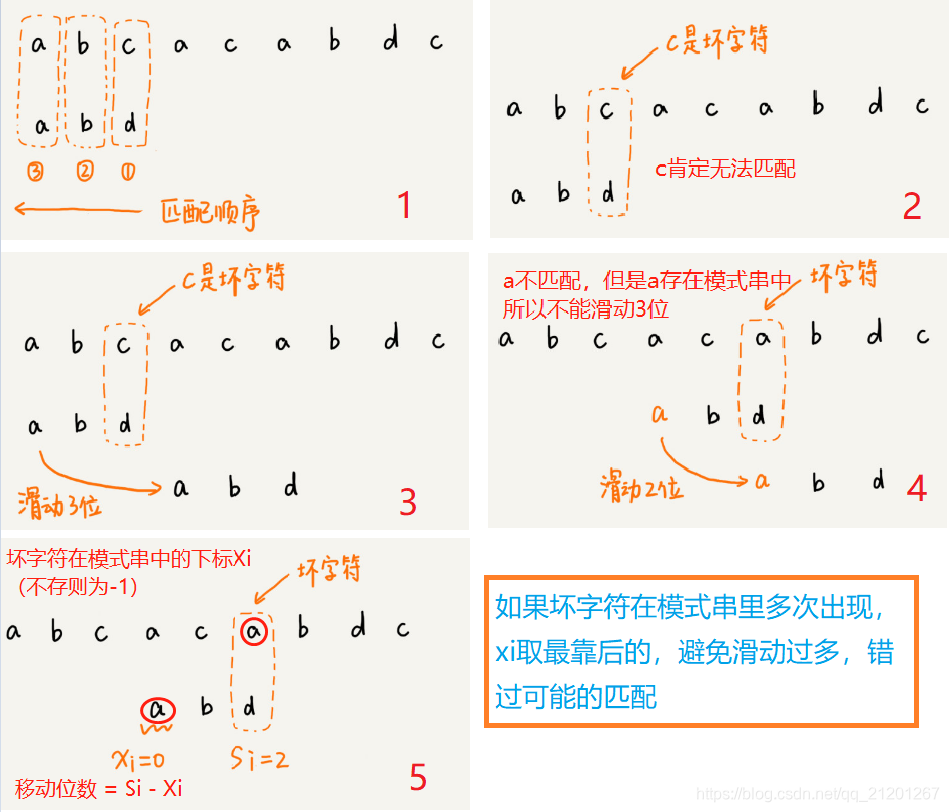
在这里插入图片描述

  • 利用坏字符规则，BM算法在最好情况下的时间复杂度非常低，是O（n/m）。比如，主串是aaabaaabaaabaaab，模式串是aaaa。每次比对，模式串都可以直接后移四位，所以，匹配具有类似特点的模式串和主串的时候，BM算法非常高效。
  • 单纯使用坏字符规则还是不够的。因为根据 si-xi计算出来的移动位数，有可能是负数，比如主串是aaaaaaaaaaaaaaaa，模式串是baaa。不但不会向后滑动模式串，还有可能倒退。所以，BM算法还需要用到“好后缀规则”。

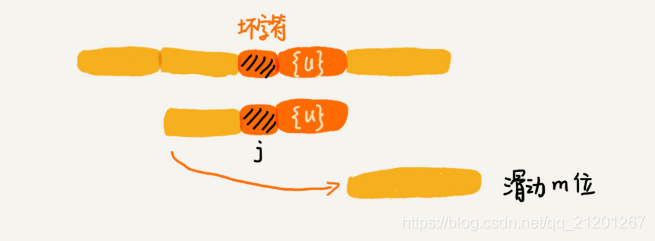
1.2 好后缀规则

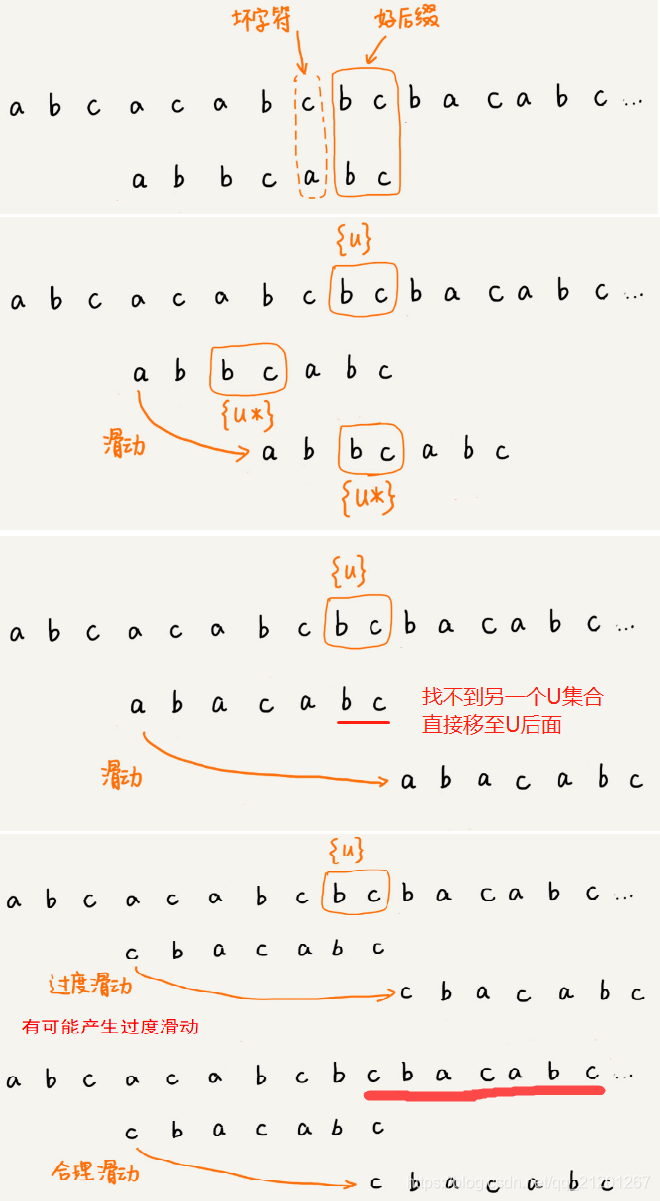
在这里插入图片描述
从好后缀的后缀子串中，找一个最长的且和模式串的前缀子串匹配的 {v}，滑动至 {v} 对齐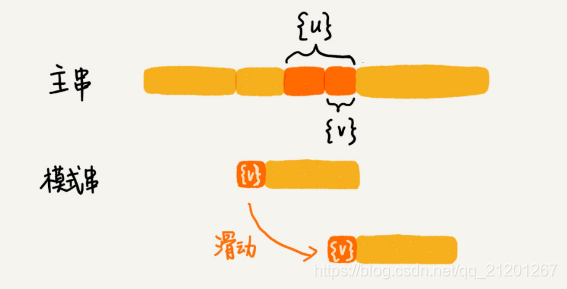
在这里插入图片描述

1.3 两种规则如何选择

  • 分别计算好后缀和坏字符规则往后滑动的位数，取大的，作为滑动位数（还可以避免负数）

2. BM算法代码实现

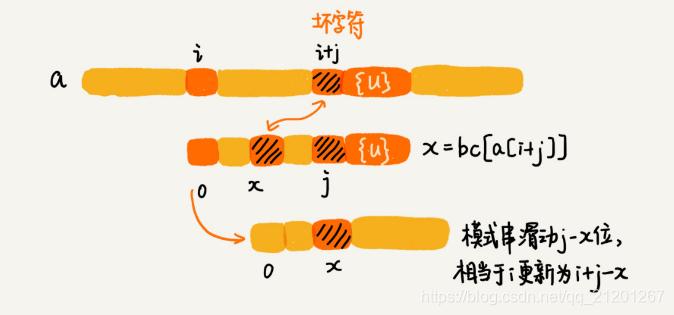
2.1 坏字符

  • 找到坏字符在模式串中的位置(有重复的，则是靠后的那个)
    采用哈希，而不是遍历。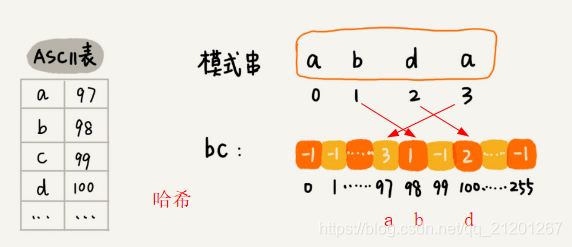
    在这里插入图片描述
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#define SIZE 256    //字符集字符数
void generateBadChar(char *b, int m, int *badchar)//(模式串字符b，模式串长度m，模式串的哈希表)
{
    int i, ascii;
    for(i = 0; i < SIZE; ++i)
    {
        badchar[i] = -1;//哈希表初始化为-1
    }
    for(i = 0; i < m; ++i)
    {
        ascii = int(b[i]);  //计算字符的ASCII值
        badchar[ascii] = i;//重复字符被覆盖，记录的是最后出现的该字符的位置
    }
}
1234567891011121314

在这里插入图片描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int str_bm(char *a, int n, char *b, int m)
//只考虑坏字符方法的程序框架
{
    int *badchar = new int [SIZE];//记录模式串中每个字符最后出现的位置
    generateBadChar(b,m,hash);     //构建坏字符哈希表
    int i = 0, j;
    while(i < n-m+1)
    {
        for(j = m -1; j >= 0; --j)  //模式串从后往前匹配
        {
            if(a[i+j] != b[j])
                break;  //坏字符对应模式串中的下标是j
        }
        if(j < 0)   //匹配成功
        {
            return i;   //返回主串与模式串第一个匹配的字符的位置
        }
        //这里等同于将模式串往后滑动 j-badchar[int(a[i+j])] 位
        i = i + (j - badchar[int(a[i+j])]);
    }
    return -1;
}
12345678910111213141516171819202122

2.2 好后缀

  • 在模式串中，查找跟好后缀匹配的另一个子串
  • 在好后缀的后缀子串中，查找最长的、能跟模式串前缀子串匹配的后缀子串

不考虑效率的话，上面两个操作都可以暴力查找；
解决办法： 预先对模式串进行处理。
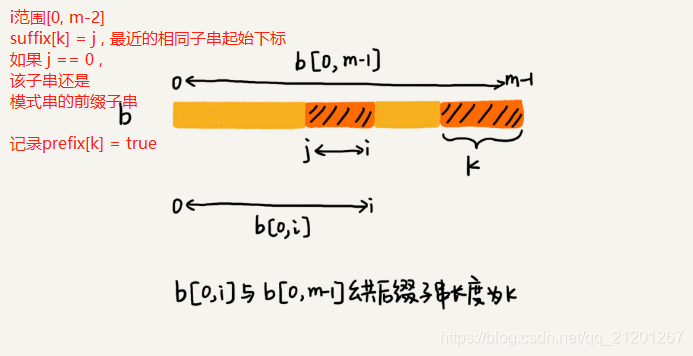
在这里插入图片描述
在这里插入图片描述
实现过程：
在这里插入图片描述
预处理模式串，填充suffix，prefix

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void generateGS(char *b, int m, int *suffix, bool *prefix)
//预处理模式串，填充suffix，prefix
{
    int i, j, k;
    for(i = 0; i < m; ++i)//两个数组初始化
    {
        suffix[i] = -1;
        prefix[i] = false;
    }
    for(i = 0; i < m-1; ++i)//b[0,i]
    {
        j = i;
        k = 0;//公共后缀子串长度(模式串尾部取k个出来，分别比较)
        while(j >= 0 && b[j] == b[m-1-k])//与b[0,m-1]求公共后缀子串
        {
            --j;
            ++k;
            suffix[k] = j+1;
            //相同后缀子串长度为k时，该子串在b[0,i]中的起始下标
            // (如果有多个相同长度的子串，被赋值覆盖，存较大的)
        }
        if(j == -1)//查找到模式串的头部了
            prefix[k] = true;//如果公共后缀子串也是模式串的前缀子串
    }
}
12345678910111213141516171819202122232425

计算滑动位数

  • case1：
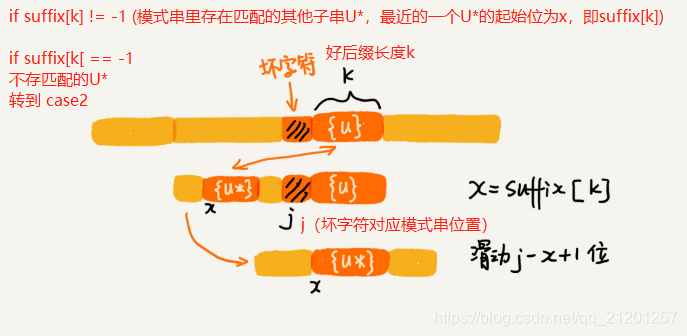
    在这里插入图片描述
  • case2：
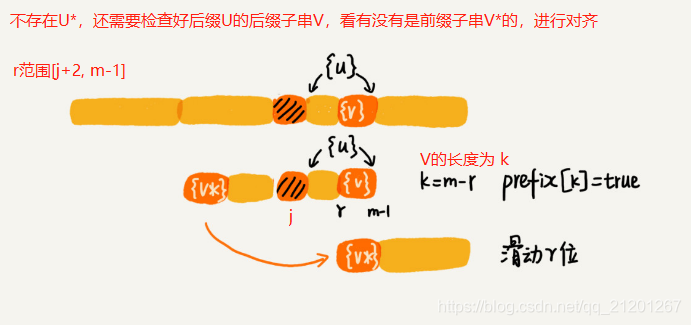
    在这里插入图片描述
  • case3：（以上都不成立，移动整个模式串（长度m））
    在这里插入图片描述

2.3 完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
/**
 * @description: 字符匹配BM算法
 * @author: michael ming
 * @date: 2019/6/18 22:19
 * @modified by: 
 */
#include <algorithm>
#include <string>
#include <iostream>

using namespace std;
#define SIZE 256    //字符集字符数
void generateBadChar(char *b, int m, int *badchar)//(模式串字符b，模式串长度m，模式串的哈希表)
{
    int i, ascii;
    for(i = 0; i < SIZE; ++i)
    {
        badchar[i] = -1;//哈希表初始化为-1
    }
    for(i = 0; i < m; ++i)
    {
        ascii = int(b[i]);  //计算字符的ASCII值
        badchar[ascii] = i;//重复字符被覆盖，记录的是最后出现的该字符的位置
    }
}
void generateGS(char *b, int m, int *suffix, bool *prefix)//预处理模式串，填充suffix，prefix
{
    int i, j, k;
    for(i = 0; i < m; ++i)//两个数组初始化
    {
        suffix[i] = -1;
        prefix[i] = false;
    }
    for(i = 0; i < m-1; ++i)//b[0,i]
    {
        j = i;
        k = 0;//公共后缀子串长度(模式串尾部取k个出来，分别比较)
        while(j >= 0 && b[j] == b[m-1-k])//与b[0,m-1]求公共后缀子串
        {
            --j;
            ++k;
            suffix[k] = j+1;
            //相同后缀子串长度为k时，该子串在b[0,i]中的起始下标
            // (如果有多个相同长度的子串，被赋值覆盖，存较大的)
        }
        if(j == -1)//查找到模式串的头部了
            prefix[k] = true;//如果公共后缀子串也是模式串的前缀子串
    }
}
int moveByGS(int j, int m, int *suffix, bool *prefix)//传入的j是坏字符对应的模式串中的字符下标
{
    int k = m - 1 - j;//好后缀长度
    if(suffix[k] != -1)//case1，找到跟好后缀一样的模式子串（多个的话，存的靠后的那个（子串起始下标））
        return j - suffix[k] + 1;
    for(int r = j + 2; r < m; ++r)//case2
    {
        if(prefix[m-r] == true)//m-r是好后缀的子串的长度，如果这个好后缀的子串是模式串的前缀子串
            return r;//在上面没有找到相同的好后缀下，移动r位，对齐前缀到好后缀
    }
    return m;//case3,都没有匹配的，移动m位（模式串长度）
}
int str_bm(char *a, int n, char *b, int m)//a表示主串，长n; b表示模式串,长m
{
    int *badchar = new int [SIZE];//记录模式串中每个字符最后出现的位置
    generateBadChar(b,m,badchar);     //构建坏字符哈希表
    int *suffix = new int [m];
    bool *prefix = new bool [m];
    generateGS(b, m, suffix, prefix);   //预处理模式串，填充suffix，prefix
    int i = 0, j, moveLen1, moveLen2;//j表示主串与模式串匹配的第一个字符
    while(i < n-m+1)
    {
        for(j = m -1; j >= 0; --j)  //模式串从后往前匹配
        {
            if(a[i+j] != b[j])
                break;  //坏字符对应模式串中的下标是j
        }
        if(j < 0)   //匹配成功
        {
            delete [] badchar;
            delete [] suffix;
            delete [] prefix;
            return i;   //返回主串与模式串第一个匹配的字符的位置
        }
        //这里等同于将模式串往后滑动 j-badchar[int(a[i+j])] 位
        moveLen1 = j - badchar[int(a[i+j])];//按照坏字符规则移动距离
        moveLen2 = 0;
        if(j < m-1)//如果有好后缀的话
        {
            moveLen2 = moveByGS(j,m,suffix,prefix);//按照好后缀规则移动距离
        }
        i = i + max(moveLen1,moveLen2);//取大的移动
    }
    delete [] badchar;
    delete [] suffix;
    delete [] prefix;
    return -1;
}

int main()
{
    string a = "abcacabcbcbacabc", b = "cbacabc";
    cout << a << "中第一次出现" << b << "的位置(从0开始)是：" << str_bm(&a[0],a.size(),&b[0],b.size());
    return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104

在这里插入图片描述

2.4 调试

为方便调试，将字符集SIZE改为3，ascii = int(b[i]-'a')

  • 坏字符在模式串中的位置（靠后的那个）
    badchar[0]：a是4
    badchar[1]：b是5
    badchar[2]：c是6
  • 预处理模式串
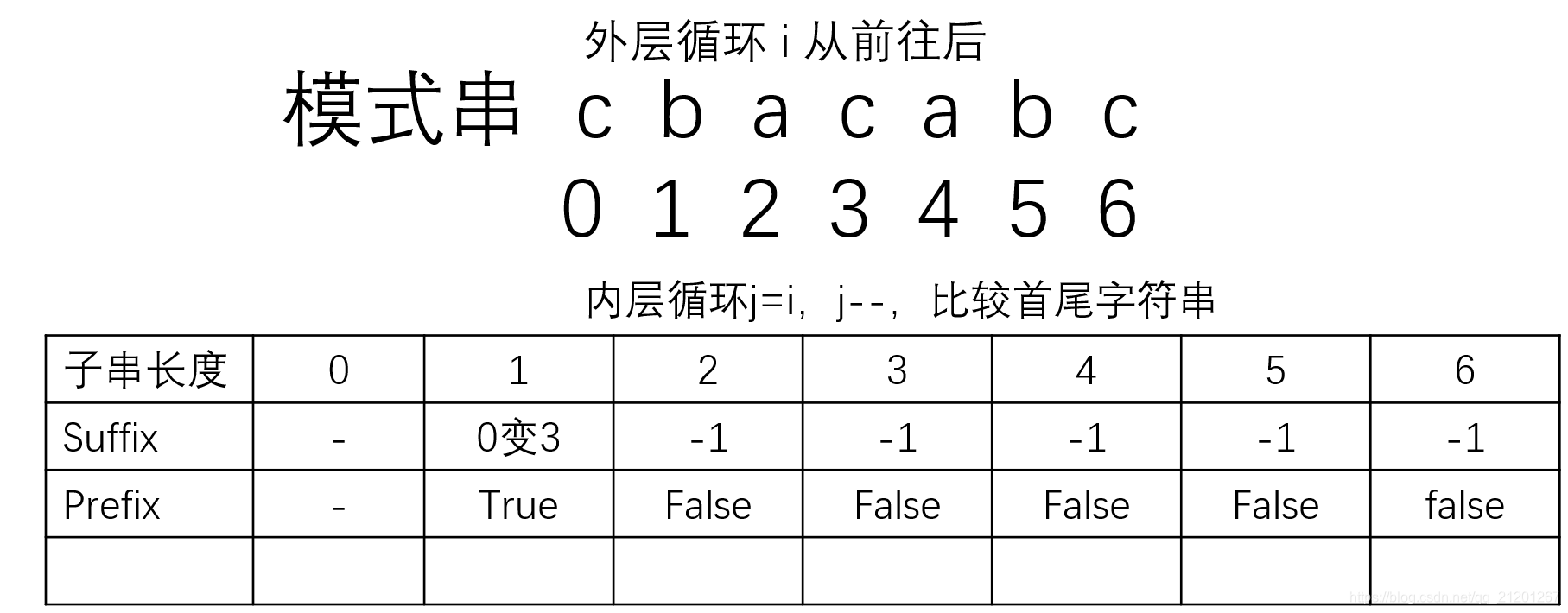
    在这里插入图片描述
  • 按规则移动
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

3. 总结

  • BM算法的内存消耗
    整个算法用到了额外的3个数组，其中bc数组的大小跟字符集大小有关，suffix数组和prefix数组的大小跟模式串长度m有关。
    如果处理字符集很大的字符串匹配问题，badchar数组对内存的消耗就会比较多。
    因为好后缀和坏字符规则是独立的，如果运行的环境对内存要求苛刻，可以只使用好后缀规则，不使用坏字符规则，就可以避免badchar数组过多的内存消耗。不过，单纯使用好后缀规则的BM算法效率就会下降一些了。
  • 时间复杂度
    以上BM算法是个初级版本。这个版本，在极端情况下，预处理计算suffix数组、prefix数组的性能会比较差。
    比如模式串是aaaaaaa这种包含很多重复的字符的模式串，预处理的时间复杂度就是O（m^2）。如何优化这种极端情况下的时间复杂度退化，以后再找空研究。
    实际上，BM算法的时间复杂度分析起来是非常复杂，论文“A new proof of the linearity of the Boyer-Moore string searching algorithm”证明了在最坏情况下，BM算法的比较次数上限是5n。论文“Tight bounds on the complexity of the Boyer-
    Moore string matching algorithm”    证明了在最坏情况下，BM算法的比较次数上限是3n。
  • BM算法核心思想是，利用模式串本身的特点，在模式串中某个字符与主串不能匹配的时候，将模式串往后多滑动几位，以此来减少不必要的字符比较，提高匹配的效率。
  • BM算法构建的规则有两类，坏字符规则和好后缀规则。
  • 好后缀规则可以独立于坏字符规则使用。
  • 因为坏字符规则的实现比较耗内存，为了节省内存，我们可以只用好后缀规则来实现BM算法。