查并集

Posted on | In | | Visitors:
Words count in article: 1.9k

并查集模板

一拖再拖，总结一下吧 : )

并查集常常用于处理一些合并和查询的问题，其中合并（union）和查询（find）是其最基本的两种操作，并查集算法主要有两种，一种是quick find，另一种quick union，顾名思义，就是分别跟倾向于其中一种操作。从一个题目入手，简要说明一下这个算法，并且给出解题的通用模板！

1. 解题模板

1.1 例题

题目链接：洛谷 P1551 亲戚

题目背景

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

题目描述

规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。

输入格式

第一行：三个整数n,m,p，（n<=5000,m<=5000,p<=5000），分别表示有n个人，m个亲戚关系，询问p对亲戚关系。

以下m行：每行两个数Mi，Mj，1<=Mi，Mj<=N，表示Mi和Mj具有亲戚关系。

接下来p行：每行两个数Pi，Pj，询问Pi和Pj是否具有亲戚关系。

输出格式

P行，每行一个’Yes’或’No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。

（具体测试样例可以去洛谷网站上去看看~）

1.2 解题思路

其实解题思路非常简单，就是将n个人划分为不同的集合，集合内的人就都是互相为亲戚关系了，整个解题的过程也就涉及到两个基本的操作，合并（输入一对对亲戚关系时合并）和查找（判断两人是否有亲戚关系时）

解决该问题可以使用如下的通用接口

ByhBAP.png

下面分别介绍两种解法~

1.2.1 quick-find

quick-find的思路非常简单，我们建立一个长度为 n 的数组 id[n]，我们先将每一个 id[i] 初始化为 i， 然后当我们合并结点时，我们就将他们的 id[i] 置为相等，如下（分为三个集合 ： {0, 5, 6}, {1, 2, 7}, {3, 4, 8, 9}）

By4AHI.png

  • 这样当我们进行查找操作时（即判断两个结点是否连接），只需要比较两个结点对应的 id 值即可（比如判断 i, j 两个结点是否连接，就是判断 id[i] 和 id[j] 是否相等即可），时间复杂度为 $O(1)$，非常高效。

  • 但是当我们进行合并操作时（合并两个集合），我们需要将其中一个集合的 id 值全部修改为另一个集合的 id 值，并且查找一个集合的所有元素只能通过遍历 id 数组来实现（可以参考下图栗子），所以合并操作的时间复杂度为 $O(n)$ ，比较慢

By5JLd.png

有了上述思路，我们就可以按照通用接口写出quick-find算法了~

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<iostream>
using namespace std;
#define N 1000
int id[N], n = 0;
void init() {	// 初始化id值
	for (int i = 1; i <= n; i++)
		id[i] = i;
}
void unionNode(int p, int q) {	// 合并节点
	int temp = id[p];
	if(temp != id[q])
		for (int i = 1; i <= n; i++) {
			if (id[i] == temp)
				id[i] = id[q];
		}
}
int find(int i) {	// 查找节点集合
	return id[i];
}
bool connected(int p, int q) {	// 判断节点是否连接
	return find(p) == find(q);
}
int main()
{
	int m, p, x, y;
	cin >> n >> m >> p;
	init();
	for (int i = 0; i < m; i++) {
		cin >> x >> y;
		unionNode(x, y);
	}
	for (int i = 0; i < p; i++) {
		cin >> x >> y;
		if (connected(x, y))
			cout << "Yes" << endl;
		else
			cout << "No" << endl;
	}
	return 0;
}

1.2.2 quick-union

为了降低合并（union）的时间复杂度，quick-union算法不是直接使用一个数组作为标记一个集合的tag，而是使用树来表示一个集合（当然树可能就是用数组实现的），我们将同一个集合中的元素合并在同一颗树下。

  • 当我们进行查找操作时，我们就只需要判断两个节点其对应的两个根节点是不是同一个（根节点是同一个就说明是同一颗树下，也就是是同一个集合），由于树的特性，这个过程的时间复杂度为 $log(n)$
  • 当我们进行合并操作时，我们只需要将一棵树链接到另一颗树上即可（作为子树），但是合并之前我们一般先查找根结点，如果根节点不同，再将一个根节点作为子节点链接上，所以时间复杂度也为 $log(n)$

关于优化

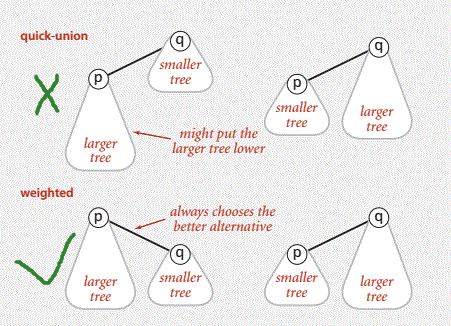
优化一：按秩合并

为了减少查找时的时间开销，我们希望减少我们树的高度，所以我们在合并的时候希望将深度更小的树作为深度更大的树的子节点，这样就能有效的降低树的高度。所以我们需要记录每棵树的深度，记作depth，如下图所示：

B6CwtK.png

优化二：路径压缩

另外我们在查找根节点的时候也可以缩短树的高度，有两种方式：① 找到某个节点的根节点后，直接将该节点链接到根节点上，作为根的直接子节点，降低树的高度；② 查找某个节点的根节点时，是一个不断的向上寻找父亲节点的过程，这个过程中可以不断的将一个节点的父亲节点修改为爷爷节点（即父亲的父亲），这样也能有效的降低高度。

可能上述两个优化有点懵，其实非常好懂，可以参考下面的代码，很简单直接~

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include<iostream>
using namespace std;
#define N 1000
int parent[N], depth[N];
void init(int n) {
	for (int i = 0; i <= n; i++) {
		parent[i] = i;	// 初始定义各个结点都为根节点
		depth[i] = 1;	// 初始定义树的深度都为1（即树结点数量）
	}
}
// **********优化点二**********
// 不优化的find
//int find(int i) {
//	while (i != parent[i]) {
//		i = parent[i];	// 向上找父结点
//	}
//	return i;
//}

// 使用方式一优化，将查找节点直接链接到根节点上
//int find(int i) {
//	if (i != parent[i]) {
//		parent[i] = find(parent[i]);	// 递归的一个过程
//	}
//	return parent[i];
//}
// 使用方式二优化  不断将父亲节点修改为爷爷节点
int find(int i) {
	while (i != parent[i]) {
		parent[i] = parent[parent[i]];
		i = parent[i];	// 向上找父结点
	}
	return i;
}
bool connected(int p, int q) {
	p = find(p);
	q = find(q);
	return p == q;
}
void unionNode(int p, int q) {
	p = find(p);
	q = find(q);
	// **********优化点一**********
	if (p == q)	// 根节点相同
		return;
	else if (depth[p] > depth[q]) {
		parent[q] = p;	// p的深度更大，将q作为子树
	}
	else if(depth[p] < depth[q]){
		parent[p] = q;	// q的深度更大，将p作为子树
	}
	else {
		parent[q] = p;	// 两棵树的深度相同，随意合并 ，但是此时需要更新树的深度
		depth[p]++;
	}
}
int main() {
	int n, m, p, temp1, temp2;
	cin >> n >> m >> p;
	init(n);
	for (int i = 0; i < m; i++) {
		cin >> temp1 >> temp2;
		unionNode(temp1, temp2);
	}
	for (int i = 0; i < p; i++) {
		cin >> temp1 >> temp2;
		if(connected(temp1, temp2))
			cout << "Yes" << endl;
		else
			cout << "No" << endl;
	}
	return 0;
}