序列合并(洛谷P1631)

Posted on | In | | Visitors:
Words count in article: 1.1k

序列合并(洛谷P1631)

清晰的记得自己做过这一题，甚至还转载过大佬的做法，好家伙，今天碰到，又不会了，淦！！ : (

序列合并

题目链接

题目描述

有两个长度都是N的序列A和B，在A和B中各取一个数相加可以得到N^2 个和， 求这N^2 个和中最小的N个。

输入格式

第一行一个正整数N；

第二行N个整数Ai, 满足Ai<Ai+1 ，且Ai<10^9;

第三行N个整数Bi, 满足Bi<Bi+1 ，且Bi<10^9;

【数据规模】

对于50%的数据中，满足1<=N<=1000；

对于100%的数据中，满足1<=N<=100000。

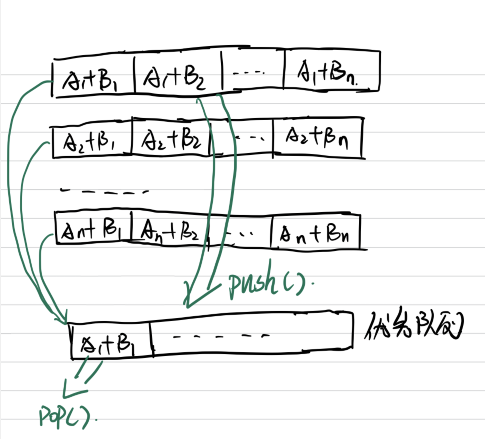
我们可以将这 $N^2$ 个数看成n个有序表，如下：

  • $A[1]+B[1] \le A[1] + B[2] \le …\le A[1]+B[n]$
  • $A[2]+B[1] \le A[2] + B[2] \le …\le A[2]+B[n]$
  • …
  • $A[n]+B[1] \le A[n] + B[2] \le …\le A[n]+B[n]$

于是我们的问题就是一个K路归并问题了，即在n个有序序列中取出前n大的数，我们可以使用一个长为n的优先队列（这里使用小顶堆），依次放入n个有序序列的首元素，然后取出优先队列首元素，然后放入其有序序列的下一个元素，重复次操作n次，就取出了最小的n个值~

BwWzgx.png

算法复杂度分析：初始建立优先队列，复杂度为$O(nlog(n))$，之后每次维护优先队列，复杂度为$O(log(n))$，共需维护$n$次，所以复杂度为$O(nlog(n))$，所以总的算法时间复杂度也为$O(nlog(n))$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<iostream>
#include<map>
#include<queue>
#include<limits.h>
#include<algorithm>
#include<vector>
#define N 110000
int A[N], B[N], index[N] = { 0 };
using namespace std;
int main()
{
	int n, temp;
	cin >> n;
	priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > que;
	for (int i = 0; i < n; i++) {
		cin >> A[i];
	}
	for (int i = 0; i < n; i++) {
		cin >> B[i];
	}
	sort(A, A + n);
	sort(B, B + n);
	for (int i = 0; i < n; i++) {
		que.push(make_pair(A[i] + B[0], i));
	}
	for (int i = 0; i < n - 1; i++) {
		cout << que.top().first << " ";
		temp = que.top().second;
		que.pop();
		que.push(make_pair(A[temp] + B[++index[temp]], temp));
	}
	cout << que.top().first << endl;
	return 0;
}

双倍经验

最小函数值

题目描述

有 n 个函数，分别为 $F_1,F_2,…,F_n$。定义 $F_i(x)=A_ix^2+B_ix+C_i(x\in N^*)$。给定这些 $A_i$、$B_i$ 和 $C_i$，请求出所有函数的所有函数值中最小的 m 个（如有重复的要输出多个）。

输入格式

第一行输入两个正整数 n 和 m。

以下 n 行每行三个正整数，其中第 i 行的三个数分别为 $A_i$、$B_i$ 和 $C_i$。

输出格式

输出将这 n 个函数所有可以生成的函数值排序后的前 m 个元素。这 m 个数应该输出到一行，用空格隔开。

数据规模与约定

对于全部的测试点，保证 $1 \le n,m\le 10000$，$1 \le A_i \le 10,B_i\le 100,C_i \le10^4$。

这一题也是一个k路合并问题，观察题目给定的数据规定不难看出，函数 $F_i(x)=A_ix^2+B_ix+C_i(x\in N^*)$在定义域内是单调递增的，所以我们的k个有序序列自然就轻松的构建出来了~ 然后就是k路合并的常规解法 : )

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<iostream>
#include<map>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
#define N 11000
int index[N][3], pos[N];
int main()
{
	int n, m, temp;
	cin >> n >> m;
	for (int i = 0; i < n; i++) {
		cin >> index[i][0] >> index[i][1] >> index[i][2];
	}
	fill(pos, pos + n, 1);
	priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > que;
	for (int i = 0; i < n; i++) {
		que.push(make_pair(index[i][0] + index[i][1] + index[i][2], i));
	}
	for (int i = 0; i < m - 1; i++) {
		cout << que.top().first << " ";
		temp = que.top().second;
		que.pop();
		pos[temp]++;
		que.push(make_pair(index[temp][0] * pos[temp] * pos[temp] + index[temp][1] * pos[temp] + index[temp][2], temp));
	}
	cout << que.top().first << endl;
	return 0;
}