背包九讲(二)——完全背包问题

Posted on | In | | Visitors:
Words count in article: 1.3k

背包九讲(二)——完全背包问题

参考了著名的背包九讲，可以在这里下载，绪前一篇的01背包问题

1.1 问题

有N种物品和一个容量为V的背包，每种物品都有无限件可用，放入第i件物品的费用是$C_i$，得到的价值是$W_i$。求解将哪些物品装入背包可使价值综合最大。

1.2 解题思路

完全背包和01背包唯一的区别就在于一件物品是否能多次选择？

知道这个区别，其实仔细一想，就能完全背包问题转化为01背包，因为容量V是有限的，对于单个物品$C_i$来说，最多只能放如$\left \lfloor V/C_i\right \rfloor$件，所以我们只需要将完全背包问题看成是有$\left \lfloor V/C_1\right \rfloor$件物品$C_1$、有$\left \lfloor V/C_2\right \rfloor$件物品$C_2$、…、$\left \lfloor V/C_N\right \rfloor$件物品$C_N$的01背包问题就可以了。但是此时总的复杂度可以认为是$O(NV\sum \cfrac{V}{C_i})$，这个复杂度有点高了~

更进一步，我们其实有更加高效的转化方法，用二进制的思想，我们可以将第 i 种物品拆解为费用为$C_i2^K$，价值为$W_i2^k$的若干件物品，其中k取1至$C_i2^k \le V$的最大整数（其实k可以取所有i种物品费用和小于V的整数），然后时间复杂度就可以优化为$O(NVlog(\left \lfloor V/C_2\right \rfloor))$了。相比之前低了不少~

当然，最nb的解法都不是上面说的hhh，在求解01背包问题时需要要求 $v$ 按照递减的顺序从 $V,V-1,..,0$ 计算 $dp[v]$ ，让 v 递减计算是为了保证状态$dp[v]$是由上一轮递推而来的，其实也就是保证一件物品只被选择一次，但是现在允许选择多次了，岂不美哉~ 非常简单，让 v 递增计算dp[v]即可，请参考下面伪代码：

1
2
3
4
dp[0...V] ← 0
for i ← 1 to N  // 依次遍历N件物品
	for v ← Ci to V // 能装下当前物品的背包使用状态方程
		dp[v] ← max{dp[v], dp[v-Ci]+Wi}

所以此时问题的时间复杂度已经降到了$O(NV)$了，秒啊~

但是完全背包就不存在01背包里的那个常数优化了~

一个简单有效的优化，若两件物品 i，j 满足$C_i \lt C_j$并且$W_i \ge W_j$，那么可以直接将物品 j 直接去掉，这个过程可以在$O(N^2)$的时间复杂度内实现，并不是很高，如果被卡时间了，可以试试这个简单的优化~

1.3 示例代码

懒得写了~还得自己造数据，和01背包问题代码类似的

1.4 实战阶段

做几道题就清楚辣！！

洛谷P1616 疯狂的采药

题目描述：

LiYuxiang 是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同种类的草药，采每一种都需要一些时间，每一种也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是 LiYuxiang，你能完成这个任务吗？

此题和原题的不同点：

  1. 每种草药可以无限制地疯狂采摘。

  2. 药的种类眼花缭乱，采药时间好长好长啊！师傅等得菊花都谢了！

具体输入输出格式以及样例请参考原题网站~

这就是一个典型的完全背包问题，直接按照上面的思路写就可以，但是这题的数据量是比较大的，注意dp数组使用long long类型，以及动态生成数组防止内存爆炸，还有就是STL是在太慢了~用malloc吧~

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int main() {
	ios::sync_with_stdio(false), cin.tie(NULL);
	// 静态数组会爆内存
	//int V[N] = { 0 }, C[N] = { 0 }, t, m;
	//long long dp[N] = { 0 };

	int t, m;
	cin >> t >> m;
	int* V = (int*)malloc(m * sizeof(int));
	int* C = (int*)malloc(m * sizeof(int));
	long long* dp = (long long*)malloc((t+1) * sizeof(long long));
	// STL太慢了
	//vector<int> V(m);
	//vector<int> C(m);
	//vector<long long> dp(t+1);
	for (int i = 0; i < m; i++) {
		cin >> C[i] >> V[i];
	}
	for (int i = 0; i < m; i++) {
		for (int j = C[i]; j <= t; j++) {
			dp[j] = max(dp[j], dp[j - C[i]] + V[i]);
		}
	}
	cout << dp[t] << endl;
	free(V);
	free(C);
	free(dp);
	return 0;
}

提交结果：

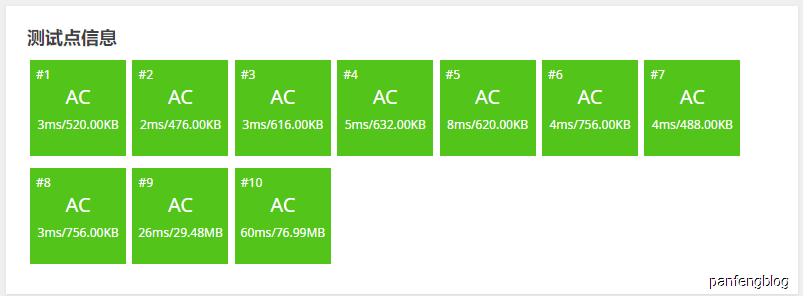
07Kye1.png

如果使用STL。。。。

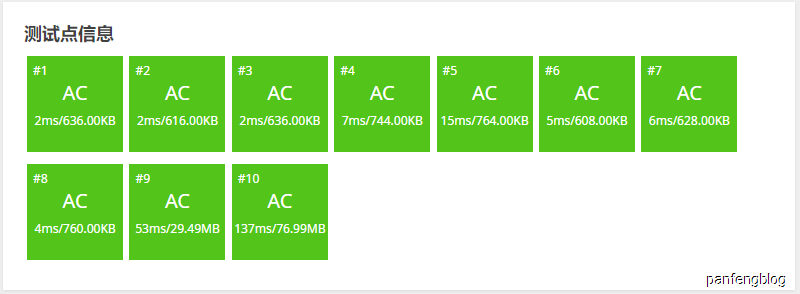
07KWWD.png

STL是malloc的两倍了~当然这里不卡时间没有啥影响