背包九讲(一)——01背包问题

Posted on | In | | Visitors:
Words count in article: 2.7k

背包九讲(一)——01背包问题

参考了著名的背包九讲，可以在这里下载，在这里做一个个人笔记，当然过程中有些不懂的地方也参考了许多其他博客，如果能帮助到你那就更好了^ ^

1.1 问题

有N件物品和一个容量为V的背包，放入第i件物品的费用是$C_i^1$，得到的价值是$W_i$。求解将哪些物品装入背包可使价值综合最大。

1.2 解题思路

最基础的背包问题，每种物品只有一件，可以选择放或者不放。

用子问题来获取状态方程：即 $F[i, j]$ 表示前 $i$ 件物品恰放入一个容量为 $v$ 的背包可以获得的最大价值。

可能刚开始看到这个方程会比较懵，接下来通过一个实例来理解一下，这个栗子参考了这篇博客（帮助很大）。

假设我们有一个可以装下4磅东西的背包，可以装的物品如下：

ajYSrn.png

当然可以选择暴力解法，穷举所有可能的装法（当然会有很多装法超出容量），然后选择价值最大的装法。每个商品都有两种状态（装或不装），所以算法的时间复杂度为$O(2^N)$，显然不合理。

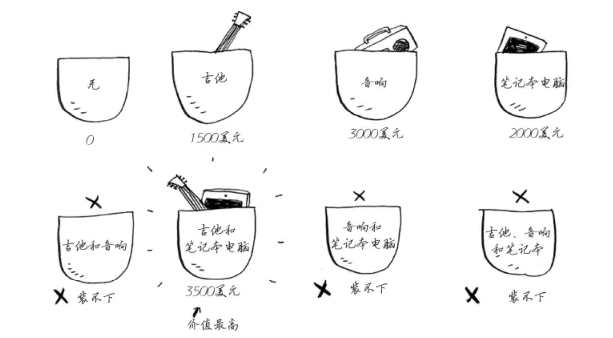
ajYE24.png

然后就是动态规划解法，将装满一个大背包转化为装满一个小背包的问题。

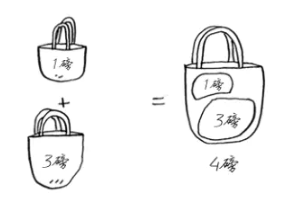
ajY4iT.png

从上面我们的状态转移方程就能看出，求解的过程就是填写一个网格（二维数组），当将网格填写完整后，我们的问题也就解决了。我们当前问题的网格如下：

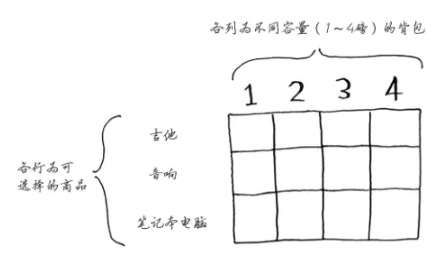
ajtNpF.png

我们接下来依次填写各行。

① 首先是吉他行，在这一行中，我们在不同背包容量情况下考虑是否装入吉他，判断的依据就是是否能够获得更高的价值。

这种情况十分简单，因为目前只有吉他一种物品，所以最优情况当然是选择装入吉他！

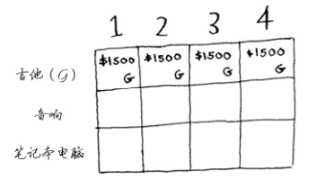
ajN9hT.png

② 其次是音响行，我们需要考虑是否装入音响，这时我们的状态转移方程就派上用场了。

由于音响为4磅，所以前三格都只能选择$dp[音响之前, v]$，如下图所示：

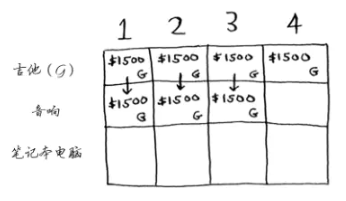
ajU4FP.png

对于第四格 $dp[音响,4] = max\left\{ 1500, 3000+ 0 \right\} = 3000$ ，即选择音响（剩余容量为0，什么也装不下）

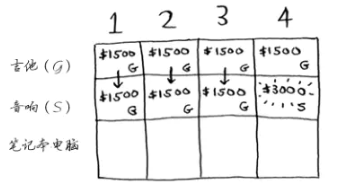
ajaNp8.png

③ 笔记本电脑行，同样的方法，使用状态方程求解。

由于笔记本为3磅，所以前两个单元格直接继承上一行的结果：

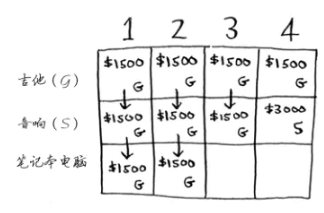
ajaxHA.png

对于第三格 $dp[笔记本电脑,3] = max\left\{ 1500, 2000+ 0 \right\} = 2000$ ，即选择音响（剩余容量为0，什么也装不下）

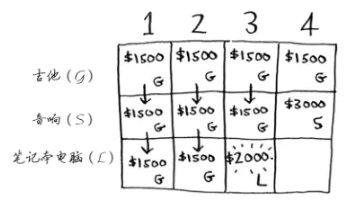
ajdnNq.png

对于第四格:

$dp[笔记本电脑,4] = max\left\{ dp[笔记本电脑之前, 4], w_{笔记本电脑}+ dp[笔记本电脑之前, 1] \right\}$

$= max\left\{ 3000, 2000+ 1500 \right\} = 3500$

然后我们就填满了表格，也就得到了最优解。

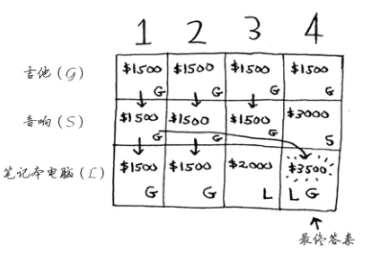
ajdcVA.png

通过这个栗子就能清楚的看到整个问题解决的过程，每当我们要选择装入一个新的物品时（当前行），我们就参考前面的结果（前一行），由此来做出决策，这样对状态转移方程也总算时理解了。

这样我们就能写出这个过程的伪代码了：

1
2
3
4
5
6
dp[0,0...V] ← 0
for i ← 1 to N  // 依次遍历N件物品
	for v ← 1 to Ci	// 装不下当前物品的背包直接继承前值
		dp[i, v] ← dp[i-1,v]
	for v ← Ci to V // 能装下当前物品的背包使用状态方程
		dp[i, v] ← max{dp[i-1,v], dp[i-1,v-Ci]+Wi}

1.3 优化空间复杂度

以上方法的时间和空间复杂度为$O(VN)$，相比较于暴力穷举 $O(2^N)$ 当然是快很多，但是还能在空间复杂度上做进一步优化。

从上面的栗子可以看出，我们考虑新的物品是否装入背包时，只需要参考前一行的结果，之前保存的结果后面都用不上了，所以我们并不需要一直保存着这样一个二维的矩阵。

并且我们看到这样一个事实，我们只参考了小于等于当前坐标的结果，即$dp[i-1, v], dp[i-1, v-C_i]$（第 $v$ 个格子和第 $v-C_i$ 个格子）

基于上面事实，我们其实只需要使用一个一维数组就能实现整个过程了，状态方程为：

但是要求 $v$ 按照递减的顺序从 $V,V-1,..,0$ 计算 $dp[v]$ ，这样就能保证整个运算过程的正确性。

此时的空间复杂度就下降到了 $O(V)$ ，但是时间复杂度并没有降低。

下面时这个过程的伪代码：

1
2
3
4
dp[0...V] ← 0
for i ← 1 to N  // 依次遍历N件物品
	for v ← V to Ci // 能装下当前物品的背包使用状态方程
		dp[v] ← max{dp[v], dp[v-Ci]+Wi}

1.4 初始化的细节问题

在上述01背包的基础上，如果要求恰好装满背包，那应该如何求解？

其实和前面的区别仅仅时初始化的方式不同。之前我们初始化就是将 $dp[0…V]$ 都初始化为0， 含义就是无论当前背包容量为多少，此时获取的最大价值为0；

而现在要求恰好装满背包，我们只需要将 $dp[0]$ 初始化为0，其余 $dp[1…V]$ 初始化为 $-\infty$ ，含义就是只有 $dp[0]$ 一个合法的解（此时恰好装满），其他情况都不是合法的解（赋值为 $-\infty$ ）。

这样就能过完美解决这样一个情况了

1.5 一个常数优化

对于不需要恰好转满背包的情况，我们最终的结果是 $dp[V]$ ，而获取这一结果我们只需要前面 $dp[V - C_N]$ 的结果，接着向前追随就只需要 $dp[V - C_N - C_{N-1}]$ 的结果，由此我们就能在一定程度上简化计算。

优化后的伪代码如下：

1
2
3
4
5
dp[0...V] ← 0
for i ← 1 to N  // 依次遍历N件物品
	bound = max(Ci, V - sum(Ci+1, Ci+2, ..., CN))
	for v ← V to bound // 能装下当前物品的背包使用状态方程
		dp[v] ← max{dp[v], dp[v-Ci]+Wi}

1.6 示例代码

代码部分：

1
2
3
4
5
6
7
8
9
int knapsack01(vector<int> weight, vector<int> value, int volume){
	vector<int> dp(volume + 1);
	for(int i = 0; i < weight.size(); i++){
		for(int v = volume; v >= weight[i]; v--){
			dp[v] = max(dp[v], dp[v-weight[i]] + value[i]);
		}
	}
	return dp[volume];
}

输入样例：

1
2
3
vector<int> weight = {4, 3, 1};
vector<int> value = {3000, 2000,1500};
int volume = 4

输出结果：

1
3500

1.7 实战阶段

学废了理论当然要选择实践一下鸭~

洛谷P1048 采药

题目描述：

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入格式和样例请参考原题~

这题完全就是一个如假包换的01背包问题，就是换了一下名词，所以直接用01背包问题的代码都行hhh

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 其实就是01背包问题的代码
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
	ios::sync_with_stdio(false), cin.tie(NULL);
	int dp[1100] = { 0 }, V[110] = {0}, C[110] = { 0 }, t, m, sumC = 0, bound;
	cin >> t >> m;
	for (int i = 0; i < m; i++) {
		cin >> C[i] >> V[i];
		sumC += C[i];
	}
	for (int i = 0; i < m; i++) {
		sumC -= C[i];
		bound = max(C[i], t - sumC);	// 这里使用了常数优化
		for (int j = t; j >= bound; j--) {
			dp[j] = max(dp[j], dp[j - C[i]] + V[i]);
		}
	}
	cout << dp[t] << endl;
	return 0;
}

洛谷P1060 开心的金明

没啥特别的一提，简单的01背包，直接上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
	ios::sync_with_stdio(false), cin.tie(NULL);
	int dp[31000] = { 0 }, C[30] = { 0 }, V[30] = { 0 }, n, m, sumC = 0, bound;
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		cin >> C[i] >> V[i];
		sumC += C[i];
	}
	for (int i = 0; i < m; i++) {
		sumC -= C[i];
		bound = max(C[i], n - sumC);
		for (int j = n; j >= bound; j--) {
			dp[j] = max(dp[j], dp[j - C[i]] + V[i] * C[i]);
		}
	}
	cout << dp[n] << endl;
	return 0;
}

洛谷P1049 装箱问题

题目描述：

有一个箱子容量为V（正整数， $0 \le V \le 20000 $ ），同时有n个物品（ $0 \lt n \le 30 $，每个物品有一个体积（正整数）。要求n个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。

输入输出格式及样例参考上述链接的题目的吧，这里就不重复了~

这里每个物品只能选取一次，显然就是一个01背包问题，但是这里的价值和经典01背包有点小区别，这里是剩余空间越来越小越好，我们只需要将 dp[i] 都初始化为 i，并且使用下面的状态转化方程即可（原来的基础上稍加修改即可）：

下面是代码部分， 应该比较好理解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<iostream>
#include<algorithm>
#include<limits.h>
using namespace std;
int main() {
	ios::sync_with_stdio(false), cin.tie(NULL);
	int dp[21000], n, C[21000] = { 0 }, V ,sumC = 0, bound;
	cin >> V;
	cin >> n;
	for (int i = 0; i <= V; i++) {
		dp[i] = i;		// 将dp[i]初始化为i
	}
	for (int i = 0; i < n; i++) {
		cin >> C[i];	// 输入物品体积
		sumC += C[i];	// 这里计算一下物品体积总和，后面用得到
	}
	for (int i = 0; i < n; i++) {
		sumC -= C[i];
		bound = max(C[i], V - sumC);	// 使用一个常数优化
		for (int j = V; j >= bound; j--) {
			dp[j] = min(dp[j], dp[j - C[i]]);	// 状态转移方程
		}
	}
	cout << dp[V] << endl;	// 输出最终结果
	return 0;
}