XGBoost原理分析

XGBoost原理分析与快速实践

1. Boosting树模型

XGBoost是Boosting树模型的一种（当然XGBoost也可以使用除树之外的其他的线性模型），其他还有许多的Boosting树模型，下面首先对Boosting树模型做一些简要的介绍。

---

给定n个样本，m个特征的数据集$D=\left\{ (X_i, y_i) \right\}(|D|=n,X_i \in R^M , y_i \in R)$，提升树模型采用K次迭代的结果做为输出结果。对于输入$X_i$，输出$\hat{y}_i$的表达式为：

$$\hat{y}_i = \phi (X_i) = \sum_{k=1}^{K} f_k(X_i),f_k \in F$$

其中$F={f(X)=\left\{ w_{q(X)} \right\}} (q:R^T \rightarrow T, w \in R^T)$，表示提升树的空间集，各个变量的含义如下：

• $q$ 表示树的结构，可以将样本映射到对应的叶子节点
• $w$ 表示树节点的权重
• $T$ 表示树叶子结点的数量
• 每个$f_k$都是一颗树，对应独立的树的结构 $q$ 和权重 $w$

---

有了上面的数学表达，我们可以通过下面这个图直观理解一下，图中就是有两个树，然后输入数据的输出是两个树的预测结果之和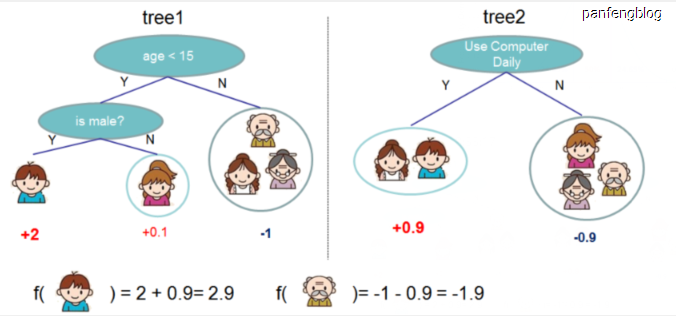

2. 目标函数

XGBoost的目标函数如下（生成第 t 棵新的树时）：

$$Obj^{(t)} = \sum_{i=1}^{n} l( y_i, \hat{y}_i^t) +\Omega(f_t)$$

符号说明：

• $l$ 为损失函数
• $\Omega$ 为正则项
• $\hat{y_i}$ 为预测标签
• $y_i$ 为真实标签
• $n$ 为样本数

---

目标函数包含两个部分，第一部分是损失函数，第二部分是正则项，首先介绍正则项，表达式如下：

$$\Omega (f) = \gamma T + \cfrac{1}{2} \lambda ||w||^2$$

符号说明：

• 其中 $T$ 为叶子结点的数量（加入该项可以控制树的复杂度，让叶子结点尽可能的少）
• $w$ 为叶子结点的权重
• $\gamma$ 和 $\lambda$ 为超参数，用于控制这两部分的权重

---

对于损失函数，当我们每次生成第 t 棵新的树时，我们会计算下面的目标函数：

$$Obj^{(t)} = \sum_{i=1}^{n} l( y_i, \hat{y}_i^{t-1} + f_t(x_i)) +\Omega(f_t)$$

然后进来泰勒展开（$f(x+\Delta x) \approx f(x) + f’(x) \Delta x + \cfrac{1}{2}f’’(x) \Delta x^2$）：

$$Obj^{(t)} = \sum_{i=1}^{n} [ l( y_i, \hat{y}_i^{t-1}) + g_i f_t(x_i) + \cfrac{1}{2} h_i f^2_i(x_i) ] +\Omega(f_t)$$

其中$g_i = \cfrac{\partial l(y_i, \hat{y}_i^{t-1})}{\partial \hat{y}_i^{t-1}}$， $h_i = \cfrac{\partial^2 l(y_i, \hat{y}_i^{t-1})}{\partial ({\hat{y}_i^{t-1}})^2}$（分别为一阶导数和二阶导数）

由于在生成第 t 棵树时，前 t-1 课树已经确定，所以$l(y_i, \hat{y}_i^{t-1})$是一个常数，所以上式又可以化简为：

$$Obj^{(t)} = \sum_{i=1}^{n} [ g_i f_t(x_i) + \cfrac{1}{2} h_i f^2_i(x_i) ] + \Omega(f_t) + constant$$

更加具体一点，当我们做分类时，我们使用logloss（当然也有其他的损失函数，取决于你的用途），如下：

$$l(\hat{y}_i, y_i) = y_i ln(1 + e^{-\hat{y}_i})+ (1- y_i) ln(1+ e^{-\hat{y}_i})$$

其中$g_i = \hat{y}_i - y_i$，$h_i = \hat{y}_i * (1 - \hat{y}_i)$

3. 求解过程

我们得到了上述的目标函数，我们需要对目标函数进行进一步的化简（这里使用的符号含义同上，没有做任何修改）：

$Obj^{(t)} \approx \sum_{i=1}^{n}[ g_i f_t(x_i) + \cfrac{1}{2} h_i f^2_i(x_i) ] + \Omega(f_t) + constant \,\,\,\, \mbox{(这里的常数项对结果没有影响，所以后面就去掉了)}$

$=\sum_{i=1}^{n} [g_i w_{q(x_i) } + \cfrac{1}{2} h_i w^2_{q(x_i)}] + \gamma T + \cfrac{1}{2} \lambda \sum_{j=1}^{T} w_j^2$

$= \sum_{j=1}^{T} [(\sum_{i \in I_j} g_i) w_j + \cfrac{1}{2}(\sum_{i \in I_j}h_i + \lambda) w_j^2] + \gamma T$

然后我们可以定义：

$$G_j = \sum_{i \in I_j} g_i \,\,\,\, H_j = \sum_{i \in I_j}h_i$$

所以上述公式可以进一步化简为：

$$Obj^{(t)} = \sum_{j=1}^{T} [G_J w_j + \cfrac{1}{2}(H_j + \lambda) w_j^2] + \gamma T$$

其中 $w_j$ 为我们待求解的权重，我们只需对 $w_j$ 求导等于0， 可以解得：

$$w_j^* = - \cfrac{G_j}{H_j+ \lambda}$$

然后将 $w_j$ 的最优解打入目标函数可以得到：

$$Obj^{(t)} = - \cfrac{1}{2} \sum_{j=1}^{T} \cfrac{G_j^2}{H_j + \lambda} + \gamma T$$

---

最后就是说，目标函数是用来衡量第 t 棵树结构的好坏的，而与叶子结点的值是没有关系的，可以从最后的公式中看出，Obj 只与 $G_j$ 、 $H_j$ 和 $T$ 有关，而他们又只与树的结构有关，和叶子结点的值无关，可以通过下图直观的理解：

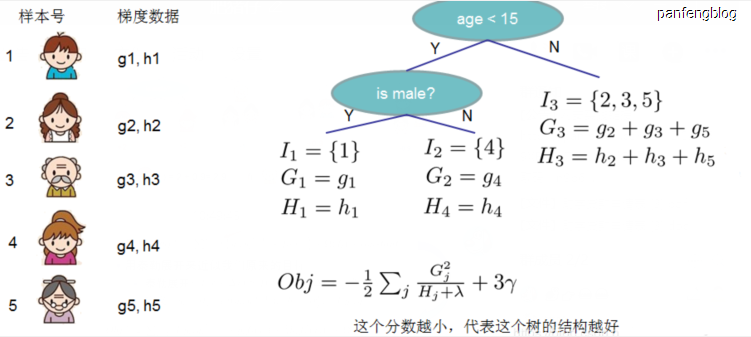
4. 寻找最佳分裂点

我们通过定义增益值来确定分裂点（和许多其他树的模型相同），以下是增益值的定义：

$$Gain = \cfrac{G_L^2}{H_L + \lambda} + \cfrac{G_R^2}{H_R + \lambda} - \cfrac{(G_L+ G_R)^2}{H_L + H_R + \lambda} - \gamma$$

符号说明：

• $G_L$ 表示划分点左边数据的一阶导数之和（$H_L \, G_R \,H_R$ 也都是类似的）
• $\gamma$ 是增加一个分支造成的复杂度增加的损失值

基于上述公式我们就有很多方案来确定最佳分裂点了

1. 贪心法：顾名思义，就是遍历所有的分割点，分别计算损失值，然后选择增益值最大的分割点（但是计算量过于巨大）
2. 近似算法：比如说三等分法，就是将数据分为三份 ，然后就会出现两个分割点，然后在这连个分割点中选择最佳分割点
3. XGBoost采用的分裂方式：使用样本的二阶导数值 $h_i$ 作为每个样本的权重，然后按照样本的权重作为依据，使用上述的三等分法，然后选择最后分割点，

---

对于XGBoost采用的分裂方式这里多说一些，为什么采用 $h_i$ 作为每个样本的权重？可以通过以下式子看到各个样本对目标函数的贡献：

---

当然对于选取分裂点时，有的样本会出现缺失值，首先是对于训练情况下：

尝试将缺失值样本划分到左节点或者右节点两种情况，然后选择增益率更大的一种情况，可以通过下面伪代码来理解一下：

然后是对于预测过程，如果遇到了缺失值，我们只需要预先制定好该节点的默认分裂方向即可。

5. 直观实践

可能看完理论分析还是会有点懵，不如自己算一遍！可以参考这篇博客，这篇文章有很多的推导过程也都是参考的这篇博客，写的非常详细！

6. 代码实践

现在已经有封装好的XGBoost实现了，只需安装一个xgboost库即可，使用的过程也非常简单，因为已经封装好了，所以内部结构对于程序员（调包侠）来说是完全透明的，我们只需要想使用决策树那样使用xgboost即可，即输入训练数据的特征已经对应的标签，然后就给你训练好了，非常的人性化~所以重点可能是在特征工程（提取出重要的特征）。当然xgboost也有许多可以调节的参数，具体可以查看相应文档，点我就可以了

下面是相应代码，使用的是Pima印第安人数据集，包含8个特征，让你预测患者是否有糖尿病（就是一个二分类）。

代码的思路非常简单，就是将8个特征和相应的标签丢进去，然后就跑出来训练后的模型，然后就能进行预测了，太方便了吧~

import numpy
import xgboost
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# load数据集
dataset = numpy.loadtxt('Pima.csv', delimiter=",")
# 把 X Y 分开
X = dataset[:,0:8]   # 特征部分
Y = dataset[:,8]     # 预测结果
# 现在我们分开训练集和测试集
seed = 7
test_size = 0.33
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=test_size, random_state=seed)
print(X.shape, Y.shape, X_train.shape, X_test.shape)
# 训练模型
model = xgboost.XGBClassifier()
# 这⾥里里参数的设置可以⻅见：https://xgboost.readthedocs.io/en/latest/python/index.html
model.fit(X_train, y_train)
# 做预测
y_pred = model.predict(X_test)
predictions = [round(value) for value in y_pred]
# 显示准确率
accuracy = accuracy_score(y_test, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))

输出结果：

(768, 8) (768,) (514, 8) (254, 8)
Accuracy: 74.02%