决策树原理分析与实践

Posted on | In | | Visitors:
Words count in article: 7.8k

决策树原理分析与实践

决策树零基础入门到实践，理论部分：会介绍决策树的生成，决策树的各种种类（ID3、C4.5、CART）以及一些数据处理（缺失值和连续值）和优化（预剪枝和后剪枝）。实践部分：以Kaggle著名的Titanic数据集（点击这里）为基础，不使用任何机器学习库完成的一颗CART决策树，并且最后进行了后剪枝操作（能看到明显的优化效果，需要完整代码和数据的可以点击这里：点我）。

原理分析

1.简要介绍

当我们判断“一个瓜是好瓜吗？”是，我们可能会想，①它是青绿色的吗？如果是的，②那么它的根蒂是否卷缩？，如果是的，③那么它的敲击声是否浊响？如果都满足，那么它大概率就是一个好瓜，这个决策的过程其实就是形成了下面一个决策树（图片采用自西瓜书）

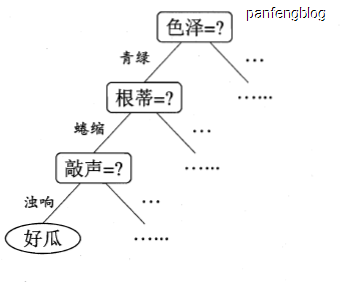
UM8G8S.png

2.决策树的生成过程

一些符号说明：

属性集：$A=\left\{ a_1,a_2,…,a_d \right\}$（假设样本共d个属性，比如上文提到的色泽、根蒂和敲声等等）

数据集：$D=\left\{ (x_1,y_1),(x_2,y_2),…,(x_m,y_m) \right\}$（假设共m个样本，$x_i$中包含样本的$d$个属性，$y_i$为类别，即保存样本是否为一个好瓜）

以下就是决策树生成的伪代码（图片采自西瓜书，加了一点笔记）：

UMtUzT.png

生成决策树就是一个递归的过程（当然很多树的构建也是这样），设置了三个递归的出口：①当类别都相同时，无需继续划分；②没有能够用来划分的属性；③当前集合以为空，当程序都没有从三个出口退出时就说明当前能够划分，然后递归调用即可。

决策树的种类有很多（ID3决策树，C4.5决策树和CART决策树等），他们的生成过程都是相同的，他的区别就是在于代码第8行处选择最优属性方法的不同（也就适用于不同的数据和场景）。

3.选择最优划分属性

3.1 信息增益（ID3决策树）

我们都听说过熵，大致是用于描述一个系统的混乱程度，在计算机领域也差不多，称为信息熵（information entropy）。

设样本集$D=\left\{ (x_1,y_1),(x_2,y_2),…,(x_m,y_m) \right\}$中有$|Y|$个类别（比如好瓜和坏瓜就两个类别），其中第$k$类样本所占比例为$p_k(k=1,2,…,|Y|)$，则其信息熵为：

$Ent(D)$的值越小，混乱程度越小，则$D$的纯度越高。

了解了信息熵后，我们开始选择最优划分属性。假设我们当前选择离散属性$a_{i}$（这里先只讨论离散属性，连续属性后面会涉及）为判断依据，属性$a_i$共有Ⅴ可能的取值$\left\{ a^1,a^2,…,a^Ⅴ \right\}$，所以就会产生Ⅴ个分支结点$D^{v}$，然后我们分别计算$D^{v}$对应的熵值$Ent(D^v)$乘以相应的权重$|D^v|/|D|$求和，$\sum_{v=1}^{Ⅴ} \cfrac{|D^v|}{|D|} Ent(D^v)$即为划分后的熵值。

划分后的熵值肯定是会增大的，直观理解的话，根据某一属性划分后纯度提升了，划分前后熵值的差即为信息增益（information gain）

我们就依次计算每个划分属性$a_i（i=1,2,…,d）$的信息增益，选择其中信息增益最大的作为最优划分属性。

3.2 增益率（C4.5决策树）

事实上，信息增益对拥有更多可能取值的属性$a_i$有所偏好，我们不妨做一个极端的假设，假设我们将样本集$D=\left\{ (x_1,y_1),(x_2,y_2),…,(x_m,y_m) \right\}$分为了m个分支结点，则$\sum_{v=1}^{Ⅴ} \cfrac{|D^v|}{|D|} Ent(D^v)=0$，那么相应的信息增益$Gain(D,a_i)=Ent(D)-\sum_{v=1}^{Ⅴ} \cfrac{|D^v|}{|D|} Ent(D^v)=Ent(D)$将达到最大，然后这样的决策树不具有泛化能力，无法对其他的新样本进行有效的预测。

所以C4.5决策树就没有采用信息增益，而是采用增益率（gain ratio），我们直接看其定义：

其中$ Ⅳ(a_i)$被称为属性$a_i$的“固有值”（intrinsic value），当属性$a_i$的可能取值$Ⅴ$越大，其$ Ⅳ(a_i)$也会越大，用信息增益除以固有值，从而消除对取值更多属性$a_i$的偏好，但是这种“消除有点过头了”，导致增益率对取值更少属性$a_i$的偏好。

所以C4.5决策树并不是直接使用的增益率，而是使用了一个启发式：在所有划分属性中找出信息增益高于平均水平的属性，然后再从中挑选增益率最高的。

3.3 基尼指数（CART决策树）

CART决策树是采用基尼指数来选用最优划分属性的，以下是基尼指数的定义（采用和3.1信息增益相同的数学符号，在此不重复声明）：

基尼指数直观反映了：随机从数据集中抽取两个样本，其类别不相同的概率。所以相应的基尼指数越小，其纯度也就越高。

同样的，当选择离散属性$a_{i}$为判断依据，属性$a_i$共有Ⅴ可能的取值$\left\{ a^1,a^2,…,a^Ⅴ \right\}$，产生Ⅴ个分支结点$D^{v}$，分别计算$D^{v}$对应的基尼指数乘以相应的权重$|D^v|/|D|$即可求的划分后的基尼指数

然后我们就只需要选取划分后基尼指数最小的属性$a_i= argmin_{1 \le i \le Ⅴ} Gini(D,a_i)$即可.

4.拓展部分

4.1 预剪枝

我们样本的属性可能非常多，如果我们严格按照上述决策树的递归生成过程会导致决策的分支过于庞大，从而导致过拟合，使得训练出来的模型泛化能力较差，所以我们就需要进行一些剪枝处理，减小整个决策树的决策分支。

我们首先将样本集分为训练集和验证集

对于预剪枝来说，就是在训练集上每次生成一个新的决策分支时（即递归生成决策树伪代码的第14行），就使用计算验证集代入计算相应的准确率，就会出现两种情况：① 生成新的决策分支导致准确率下降了，那么就能停止这次划分；② 生成新的决策分支导致准确率上升了，那么就能执行这次划分。可以参照下面这张西瓜书上的图对比一下（具体的数据duck不必在意）。

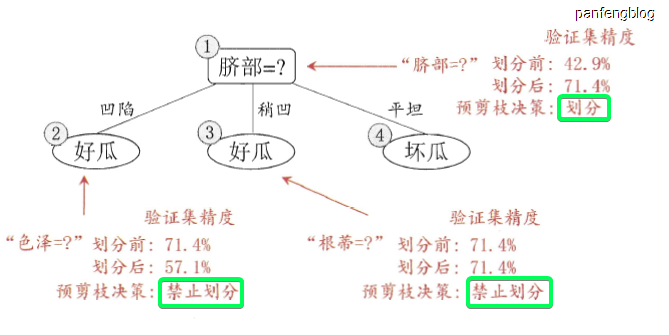
UMHj0S.png

优点：

  1. 防止过拟合
  2. 及时剪枝，中止继续递归操作，在一定程度上加快了训练速度

缺点：

  1. 也许验证集在划分后的准确率不如划分前的准确率，但是有可能划分后的后续划分可能会导致准确率的显著上升，所以预剪枝存在欠拟合的风险。

4.2 后剪枝

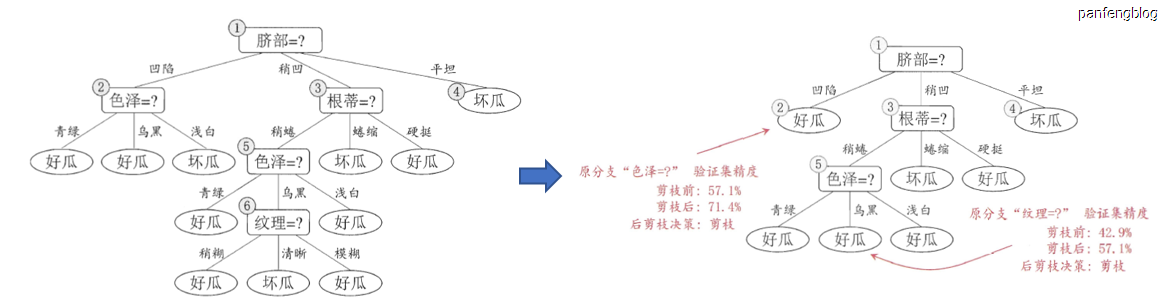
后剪枝的操作和预剪枝其实非常相似。后剪枝是在通过决策树生成的递归算法生成一颗完全的决策树后，然后自底向上，可以按照后根遍历的顺序尝试删除结点，比较去除前后的验证集准确率，如果能够提高准确率，则去除相应的划分。

下面是从西瓜书上截取的一个样例

UMqFCd.png

优点：

  1. 使用后剪枝之前，所有分支都已展开，所以不用担心欠拟合
  2. 防止过拟合（进行了剪枝操作）

缺点：

  1. 需要展开所有分支，所以生成决策树耗费时间会更多

4.3 连续值处理

前面我们提到的属性的划分都是对于离散属性而言的，然而还有一些属性不是离散的值（比如西瓜的重量、含糖量等），将连续值离散化最简单的就是采用二分法。

对于样本集$D$上的连续属性$a_i$，假设有$n$个取值，从小到大排序为$\left\{ a_i^1 , a_i^1 , … , a_i^n \right\}$，然后尝试在相邻的两点取中位数尝试划分，即所有可能划分点为$T_n = \left\{ \cfrac{a^j_i + a^{j+1}_i}{2} | 1 \le j \le n-1 \right\}$

然在计算所有划分点对应的信息增益（或是增益率、基尼指数），求出连续属性$a_i$的最佳划分点，然后再和其他的划分属性进行对比，然后再决定此次划分属性。

值得注意的是，与离散属性不同，连续属性可以多次作为划分属性（其实每次划分只使用了其一个划分中位点）。

4.4 缺失值处理

我们的数据集中可能存在缺失值，缺失值的处理相较于连续值会麻烦一点。

我们需要为每个样本$x$定义权重$w_x$（权重$w_s$初始值为1），对于样本集D和含有缺失值的划分属性$a_i$，设$\overline{D}$为$D$中属性$a_i$不是缺失值的样本集合，则可以计算下列值：

不难发现，$\sum_{k=1}^{|Y|} p_k =1 ,\sum_{v=1}^{|Y|} r_v =1$，并且当权重$w_x$初始值为1时，$p_k,r_v$和之前的定义没有什么区别。

然后使用上述公式得出$p_k , r_v$，进而计算相应的信息增益（或是增益率、基尼指数），然后将求得的信息增益乘以$ \rho $得到该划分属性最终的信息增益，再和其他划分属性进行对于，得到最终的划分属性。

如果很不幸，该含有缺失值的划分属性$a_i$被选为了最优划分属性，① 那么对于不是缺失值的样本$x$保持其权重$w_x$直接划入相应子节点，② 但是对于属性$a_i$为缺失值的样本$x$，将其划分到所有的子节点，但是其权重子节点中调整为$r_v\times w_x$，直观理解就，就是让一个样本以不同的概率划分到不同的子结点中。

进行预测时，碰到缺失值怎么办？这是我们就选择该结点下$r_v$最大的一个分支（即该属性的取值最多）。

4.5 多变量决策树

如果我们将属性看作是坐标空间的坐标轴，那么样本$x$的属性$\left\{ a^1,a^2,…,a^Ⅴ \right\}$就是其相应的坐标，决策树的分类其实就是在这个坐标空间中画出了一个分类边界。

我们以两个属性为例查看其决策边界（图片采用自西瓜书）

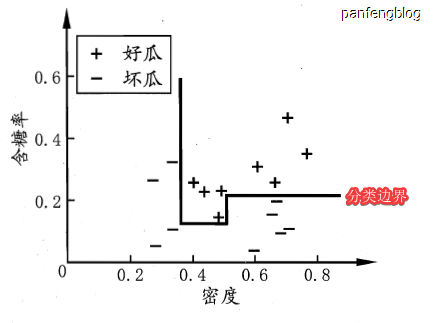
UMOwcR.png

可以看到分类边界的每一段都是和坐标轴平行的，当分类边界比较复杂时，就需要多段划分才能获得较好的划分效果。

但是我们是否一定要使用这样平行与坐标轴的边界吗？当然不是，当我们使用多个属性线性组合就能得到倾斜的决策边界，如下图（采用自西瓜书）

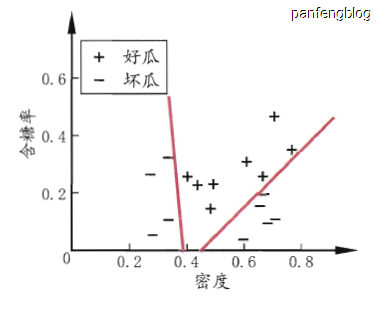
UMOrB6.png

更进一步想的话，我们是否一定要使用”平直“的决策边界？其实也不是，我们不一定使用的是多个属性的线性组合，当然也能使用非线性组合，然后就能得到如下图所示的效果（来自西瓜书）。

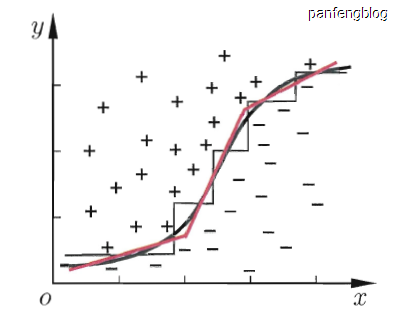
UMOcND.png

当然这里多变量决策树了解的比较浅显，具体要如何构建多变量决策树？这是一个问题，有缘再了解吧~

CART决策树实践

ID3、C4.5、CART决策树实现过程大体相同，只需更改其中的最优划分属性算法即可（相较于决策树的其它实现步骤是相对来说比较简单的），所以这里就只实践了CART决策树。需要完整代码和数据的可以点击这里：点我，这次实践主要就是不使用任何机器学习库，纯手工完成的决策树的搭建，并且完成了后剪枝操作

python3开发环境说明：

  • csv:1.0

1. 数据加载

采用的是Kaggle上的Titanic数据集（点击这里），RMS泰坦尼克号的沉没是历史上最臭名昭着的沉船之一，2224名乘客和机组人员中有1502人遇难，一个人是否能够存活下来与许多的因素有关，题目给出了一个训练数据集（train.csv）、一个需要预测的数据集（test.csv）和一个提交的模板（gender_submission.csv）。我们着重分析一下已知结果的训练数据集。

其中包含了11个特征，除去没有直接帮助的姓名特征和票号特征还剩9个特征，如下图所示（最后一项为权重，用于缺失值处理），我们将数据加载进来，按照下图的映射关系，将csv表格中的数据转化为int或float类型。

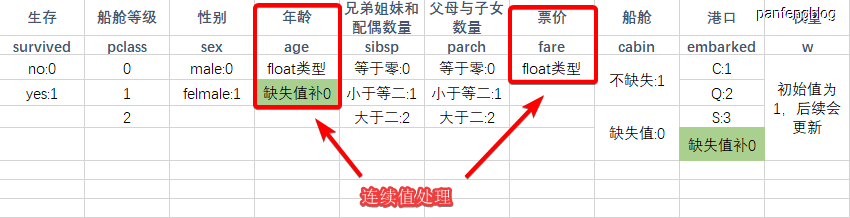
U1yZXd.png

值得注意的是：

  1. 船舱等级整体减1（便于写代码）
  2. 原本有三项特征有缺失值，但是经过分析后，船舱特征是否缺失和乘客是否存活有一定关系，所以将它的缺失与不缺失直接转化为特征值
  3. 兄弟姐妹配偶数量和父母子女数量大部分乘客都是0，少部分小于等于2，极少部分大于2，所以将多个离散值映射到了0~2

加载部分代码（按照大于 5:1 划分训练集和验证集）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def loadTrainData(filename):
    data = []
    f = list(csv.reader(open(filename, 'r')))[1:]   # 读取去掉表头的部分
    embarkedDist = {'C':1, 'Q':2, 'S':3}    # 无缺失值时，'C':1, 'Q':2, 'S':3
    sibspParch = [1, 2]
    for line in f:
        if int(line[6]) == 0:  # 转化sibsp
            sibsp = 0
        elif int(line[6]) <= 2:
            sibsp = 1
        else:
            sibsp = 2
        
        if int(line[7]) == 0:   # 转化sibsp
            parch = 0
        elif int(line[7]) <= 2:
            parch = 1
        else:
            parch = 2
        dataDist={'survived':int(line[1]),
             'pclass': int(line[2]) - 1,
             'sex': 0 if line[4] == 'male' else 1,   # male:0  female:1
             'age': 0 if len(line[5]) == 0 else float(line[5]),   # 有缺失值保存为0
             'sibsp': sibsp,
             'parch': parch,
             'fare': float(line[9]),
             'cabin': 0 if len(line[10]) == 0 else 1,   # 有缺失值：0  无缺失值：1
             'embarked': 0 if len(line[11]) == 0 else embarkedDist[line[11]],   # 有缺失值：0  无缺失值保存为1、2、3
                  'w': 1}  # 初始化权重
        data.append(dataDist)
    random.shuffle(data)     # 将加载好的数据打乱
    trainData = data[:741]  # 按大致5:1划分训练集和验证集
    devData = data[741:]
    return trainData, devData


trainData, devData = loadTrainData('train.csv')
print(len(trainData), len(devData), trainData[0])

输出结果：

1
741 150 {'survived': 0, 'pclass': 0, 'sex': 0, 'age': 19.0, 'sibsp': 2, 'parch': 1, 'fare': 263.0, 'cabin': 1, 'embarked': 3, 'w': 1}

2. 构建决策树

决策树的定义比较繁琐，由于许多划分属性的取值并不是只有两种取值，从而形成的决策树不会是一颗二叉树，所以这里的决策树是采用列表存储的孩子结点（之所以能用列表还不需要字典，是因为将属性值都转化为了[0,i]的离散值（连续值就两种情况，小于和大于），不知所云也没关系，直接看代码也能看懂）

2.1 结点定义

1
2
3
4
5
6
7
8
class Node:
    def __init__(self,attribute):
        self.son = []  # 结点的孩子
        self.attribute = attribute    # 结点当前的划分属性
        self.boundary = -1  # 当前结点划分属性为连续值时才修改该属性
        self.kind = -1    # 当前结点的种类，只有当时叶子结点时用于判定
        self.leaf = 0    # 当前结点为叶子结点时指定为1
        self.prior = 0  # 当进行决策时出现缺失值，优先选择的种类

2.2 决策树定义

这一部分代码会比较冗长，奈何本人水平有限，但是都是做了非常详细的注释，不用一次性都将所有函数读完，用到了再回头看即可。

决策树的构造函数

1
2
3
class decisionTree:
    def __init__(self):
        self.root = Node('')

递归构建决策树：由于特征种类的复杂性，所已对不同特征进行了不同的操作，因而代码显得比较冗长

递归设置了三个出口（在理论部分已经强调过了），还有就是涉及到了缺失值和连续值的处理，可以参考前文的理论部分分析。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
def createTree(self, attributes, datas): # 当前可用属性，当前可用样本，当前所在的递归层数（即在第几层结点）
    node = Node('')
    node.kind = self.getKind(datas)
    sameFlag = 1    # 标记当前样本种类是否相同
    for i in range(1, len(datas)):
        if datas[i]['survived'] != datas[0]['survived']:
            sameFlag = 0
            break
    if sameFlag == 1:        # 递归出口①：当样本属于同一类别
        node.leaf = 1
        return node
    
    delAttributes = []   # 需要删除的无效划分属性
    for a in attributes:
        if a == 'pclass' or a == 'sibsp' or a == 'parch':
            effectiveAttribute = [0, 0, 0]   # 标记当前属性是否为有效属性
            for data in datas:
                effectiveAttribute[data[a]] = 1   # 说明该属性有样本
            if effectiveAttribute[0] * effectiveAttribute[1] * effectiveAttribute[2] == 0:  # 当该属性的有一个取值无样本，则删除该属性
                delAttributes.append(a)
        elif a == 'sex' or a == 'cabin':
            effectiveAttribute = [0, 0]   # 标记当前属性是否为有效属性
            for data in datas:
                effectiveAttribute[data[a]] = 1   # 说明该属性有样本
            if effectiveAttribute[0] * effectiveAttribute[1]== 0:  # 当该属性的有一个取值无样本，则删除该属性
                delAttributes.append(a)
        elif a == 'embarked':
            effectiveAttribute = [0 , 0, 0, 0]   # 标记当前属性是否为有效属性
            for data in datas:
                effectiveAttribute[data[a]] = 1   # 说明该属性有样本
            if effectiveAttribute[1] * effectiveAttribute[2] * effectiveAttribute[3] == 0:  # 当该属性的有一个取值无样本，则删除该属性
                delAttributes.append(a)                           # 不记录缺失值
    for a in delAttributes:   # 从属性列表中删除无效属性
        attributes.remove(a)
    if len(attributes) == 0:   # 递归出口②：如果此时无有效属性
        node.leaf = 1
        return node
    
    gini, a, boundary = self.Gini(attributes, datas)
    node.attribute = a  # 当前结点使用的划分属性
    attributes.remove(a)
    
    if a == 'pclass' or a == 'sibsp' or a == 'parch':
        datasSub = [[],[],[]]  # 保存用于划分的子集
        for data in datas:
            datasSub[data[a]].append(deepcopy(data))  # 子集添加元素
        if len(datasSub[0]) == 0 or len(datasSub[1]) == 0 or len(datasSub[2]) == 0:   # 递归出口③：有一个划分样本集合为空，停止划分
            node.leaf = 1
            return node
        for i in range(3):  # 若集合都不为空，则继续递归划分
            node.son.append(self.createTree(deepcopy(attributes), datasSub[i]))
        return node
    
    elif a == 'sex' or a == 'cabin':
        datasSub = [[],[]]  # 保存用于划分的子集
        for data in datas:
            datasSub[data[a]].append(deepcopy(data))  # 子集添加元素
        if len(datasSub[0]) == 0 or len(datasSub[1]) == 0 :   # 递归出口③：有一个划分样本集合为空，停止划分
            node.leaf = 1
            return node
        for i in range(2):  # 若集合都不为空，则继续递归划分
            node.son.append(self.createTree(deepcopy(attributes), datasSub[i]))
        return node
    
    elif a == 'fare':
        node.boundary = boundary  # 由于是连续值，需要调整
        datasSub = [[],[]]
        for data in datas:
            if data[a] < boundary:
                datasSub[0].append(deepcopy(data))   # 添加相应的权重
            else:
                datasSub[1].append(deepcopy(data))   # 添加相应的权重
        if len(datasSub[0]) == 0 or len(datasSub[1]) == 0 :   # 递归出口③：有一个划分样本集合为空，停止划分
            node.leaf = 1
            return node
        for i in range(2):  # 若集合都不为空，则继续递归划分
            node.son.append(self.createTree(deepcopy(attributes), datasSub[i]))
        return node
    
    elif a == 'embarked':
        datasSub = [[],[],[]]  # 保存用于划分的子集
        missData = []  # 保存缺失值
        for data in datas:
            if data[a] != 0:
                datasSub[data[a] - 1].append(deepcopy(data))  # 子集添加元素
            else:
                missData.append(deepcopy(data))  # 添加缺失值
        length = []
        length.append(len(datasSub[0]))  # 记录各个集合的大小，用于后续计算
        length.append(len(datasSub[1]))
        length.append(len(datasSub[2]))
        lenSum = sum(length)
        lenMax = max(length)
        if length[0] * length[1] * length[2] == 0:   # 递归出口③：有一个划分样本集合为空，停止划分
            node.leaf = 1
            return node
        if lenMax == length[0]:  # 由于embarked属性有可能出现缺失值，所有要设置优先属性
            node.prior = 0
        elif lenMax == length[1]:
            node.prior = 1
        else:
            node.prior = 2
        for data in missData:  # 将缺失值调整权重加入到各个集合
            for i in range(3):
                temp = deepcopy(data)
                temp['w'] *= length[i]/lenSum   # 修改权重
                datasSub[i].append(temp)
        for i in range(3):  # 若集合都不为空，则继续递归划分
            node.son.append(self.createTree(deepcopy(attributes), datasSub[i]))
        return node
    
    elif a == 'age':
        node.boundary = boundary
        datasSub = [[],[]]
        missData = []  # 保存缺失值
        for data in datas:
            if data[a] != 0:
                if data[a] < boundary:
                    datasSub[0].append(deepcopy(data))   # 添加相应的权重
                else:
                    datasSub[1].append(deepcopy(data))   # 添加相应的权重
            else:
                missData.append(deepcopy(data))  # 添加缺失值
        length = []
        length.append(len(datasSub[0]))  # 记录各个集合的大小，用于后续计算
        length.append(len(datasSub[1]))
        lenSum = sum(length)
        lenMax = max(length)
        if len(datasSub[0]) == 0 or len(datasSub[1]) == 0 :   # 递归出口③：有一个划分样本集合为空，停止划分
            node.leaf = 1
            return node
        if lenMax == length[0]:  # 由于embarked属性有可能出现缺失值，所有要设置优先属性
            node.prior = 0
        else:
            node.prior = 1
        for data in missData:  # 将缺失值调整权重加入到各个集合
            for i in range(2):
                temp = deepcopy(data)
                temp['w'] *= length[i]/lenSum   # 修改权重
                datasSub[i].append(temp)
        
        for i in range(2):  # 若集合都不为空，则继续递归划分
            node.son.append(self.createTree(deepcopy(attributes), datasSub[i]))
        return node

获取当前样本集中最多的种类

1
2
3
4
5
6
7
8
def getKind(self, datas):
    count = 0
    for data in datas:
        count += data['survived']
    if count > len(datas)//2:
        return 1
    else:
        return 0

计算Gini指数：也是由于特征的复杂性，所以不同特征计算Gini指数会有一些差异，需要分情况讨论，所以代码显得很冗长（但是写得都很浅显 是我菜哈哈哈）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
def Gini(self, attributes, datas):
    giniList = []
    for a in attributes:
        if a == 'pclass' or a == 'sibsp' or a == 'parch':  # 这三类相似，离散属性都是三种取值
            count=[[0,0], [0,0], [0,0]]   # 用于保存该属性下存活于死亡的情况
            for data in datas:
                count[data[a]][data['survived']] += data['w']   # 添加相应的权重
            gini = 0
            for i in range(3):  # 计算基尼指数
                gini += (count[i][0] + count[i][1])/len(datas) * (1 - (count[i][1]/(count[i][0] + count[i][1]))**2)
            giniList.append(gini)
        
        elif a == 'sex' or a == 'cabin':  # 这两类相似，离散数学都是两种取值
            count=[[0,0], [0,0]]    # 用于保存该属性下存活于死亡的情况
            for data in datas:
                count[data[a]][data['survived']] += data['w']   # 添加相应的权重
            gini = 0
            for i in range(2):  # 计算基尼指数
                gini += (count[i][0] + count[i][1])/len(datas) * (1 - (count[i][1]/(count[i][0] + count[i][1]))**2)
            giniList.append(gini)
            
        elif a == 'fare':
            fareList = []
            for data in datas:
                fareList.append(data['fare'])   # 添加所有的fare
            fareList = list(set(fareList))   # 去重
            fareList.sort()
            for i in range(len(fareList) - 1):
                fareList[i] = (fareList[i] + fareList[i+1])/2   # 计算所有可能的中位值
            fareList.pop()
            gini_temp = []  # 暂存所有的gini指数
            for fare in fareList:
                count=[[0,0], [0,0]]
                for data in datas:
                    if data['fare'] < fare:
                        count[0][data['survived']] += data['w']   # 添加相应的权重
                    else:
                        count[1][data['survived']] += data['w']   # 添加相应的权重
                gini = 0
                for i in range(2):  # 计算基尼指数
                    gini += (count[i][0] + count[i][1])/len(datas) * (1 - (count[i][1]/(count[i][0] + count[i][1]))**2)
                gini_temp.append(gini)
            gini = min(gini_temp)   # 求出最小的基尼指数
            fare = fareList[gini_temp.index(gini)]   # 求出最小基尼指数相应的划分fare
            giniList.append(gini)
        
        elif a == 'embarked':
            count=[[0,0], [0,0], [0,0]]   # 用于保存该属性下存活于死亡的情况
            dataNum = 0
            for data in datas:
                if data['embarked'] != 0:  # 不是缺失值情况
                    count[data['embarked'] - 1][data['survived']] += data['w']   # 添加相应的权重
                    dataNum += 1  # 非缺失值加1
            rho = dataNum/len(datas)
            gini = 0
            for i in range(3):  # 计算基尼指数
                gini += (count[i][0] + count[i][1])/len(datas) * (1 - (count[i][1]/(count[i][0] + count[i][1]))**2)
            gini *= rho   # 乘以rho
            giniList.append(gini)
            
        elif a == 'age':
            ageList = []
            for data in datas:
                if data['age'] != 0:  # 当不是缺失值时
                    ageList.append(data['age'])   # 添加所有的age
            ageNum = len(ageList)
            rho = ageNum/len(datas)
            ageList = list(set(ageList))   # 去重
            ageList.sort()
            for i in range(len(ageList) - 1):
                ageList[i] = (ageList[i] + ageList[i+1])/2   # 计算所有可能的中位值
            ageList.pop()
            gini_temp = []  # 暂存所有的gini指数
            for age in ageList:
                count=[[0,0], [0,0]]
                for data in datas:
                    if data['age'] != 0:
                        if data['age'] < age:
                            count[0][data['survived']] += data['w']   # 添加相应的权重
                        else:
                            count[1][data['survived']] += data['w']   # 添加相应的权重
                gini = 0
                for i in range(2):  # 计算基尼指数
                    gini += (count[i][0] + count[i][1])/len(datas) * (1 - (count[i][1]/(count[i][0] + count[i][1]))**2)
                gini *= rho   # 乘以rho
                gini_temp.append(gini)
            gini = min(gini_temp)   # 求出最小的基尼指数
            age = ageList[gini_temp.index(gini)]   # 求出最小基尼指数相应的划分age
            giniList.append(gini)
        
        gini = min(giniList)  # 求出所有划分可能中最小的基尼指数
        a = attributes[giniList.index(gini)]  # 求出对应的划分属性
        
        if a == 'age':
            return gini, a, age # 连续值情况下，返回对应的划分边界
        elif a =='fare':
            return gini, a, fare # 连续值情况下，返回对应的划分边界
        else:
            return gini, a, 0

预测函数：构建好了决策树后用于预测（注意预测过程中，样本缺失值的处理，忘了可以查看前文缺失值的处理）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def predict(self, node, predictData):
    if node.leaf == 1:  # 当前结点为叶子结点时
        return node.kind
    else:
        a = node.attribute
        if a == 'embarked':
            if predictData[a] == 0:    # 当前结点此值为缺失值时
                return self.predict(node.son[node.prior], predictData)
            else:  # 如果不是缺失值，则按属性划分
                return self.predict(node.son[predictData[a] - 1], predictData)
        elif a == 'fare':
            if predictData[a] < node.boundary:   # 连续值处理
                return self.predict(node.son[0], predictData)
            else:
                return self.predict(node.son[1], predictData)
        elif a == 'age':
            if predictData[a] == 0:        # 当前结点此值为缺失值
                return self.predict(node.son[node.prior], predictData)
            else:
                if predictData[a] < node.boundary:   # 连续值处理
                    return self.predict(node.son[0], predictData)
                else:
                    return self.predict(node.son[1], predictData)
        else:
            return self.predict(node.son[predictData[a]], predictData)

后剪枝：这部分包含了两个函数，一个用于获取后根遍历的所有路径，一个根据获取的路径来依次尝试删除结点，并且比较输入准确率的大小，从而决定是否剪枝。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def postOrderTraverse(self, node, route, traverseList):  # 后根遍历所有的非叶子结点
    for i in range(len(node.son)):
        if node.son[i].leaf != 1:
            temp_route = deepcopy(route)  # 如果其子节点不是叶子结点，则继续递归访问
            temp_route.append(i)
            self.postOrderTraverse(node.son[i], temp_route, traverseList)
    traverseList.append(route)   # 最后添加当前结点路径
def postPruning(self, curAccuracy, devData):   # 后剪枝
    traverseList = []
    self.postOrderTraverse(node = self.root, route = [],traverseList = traverseList)   # 获取后根遍历的路径
    tempNode = Node('')
    for route in traverseList:  # 依次遍历路径，按照后根遍历的顺序进行后剪枝
        tempNode = self.root
        for i in route:
            tempNode = tempNode.son[i]  # 遍历到目标结点
        tempNode.leaf = 1
        count = 0
        for data in devData:
            if data['survived'] == cartTree.predict(cartTree.root, data):
                count +=1
        Accuracy = count/len(devData)  # 计算当前在验证集上的正确率
        if Accuracy <= curAccuracy:  # 如果正确率降低了，那么撤回修改
            tempNode.leaf = 0
        else:
            curAccuracy = Accuracy  # 如果正确率上升了，执行修改并且更新当前的准确率

决策树可视化：一个十分简陋的决策树可视化

1
2
3
4
5
6
7
8
9
def showTree(self, node, layer):
    if node.leaf == 0:
        show_str = str(layer)
        for i in range(layer):
            show_str += '-*'
        show_str += node.attribute
        print(show_str)
    for son in node.son:
        self.showTree(son, layer+1)

2.3 决策树初始化

决策树类都定义好了，就开始初始化吧

1
2
3
cartTree = decisionTree()
cartTree.root = cartTree.createTree(attributes = ['pclass', 'sex', 'age', 'sibsp', 'parch', 'fare', 'cabin', 'embarked'], datas = trainData)
cartTree.showTree(cartTree.root, 1)  # 查看决策树

输出结果（前面的数字代表在第几层，最后表示当前结点的最优划分属性）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
1-*pclass
2-*-*sex
3-*-*-*age
4-*-*-*-*fare
5-*-*-*-*-*cabin
4-*-*-*-*sibsp
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
6-*-*-*-*-*-*cabin
5-*-*-*-*-*parch
6-*-*-*-*-*-*fare
7-*-*-*-*-*-*-*cabin
6-*-*-*-*-*-*fare
3-*-*-*age
4-*-*-*-*fare
4-*-*-*-*sibsp
5-*-*-*-*-*fare
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
2-*-*sex
3-*-*-*age
4-*-*-*-*fare
5-*-*-*-*-*cabin
4-*-*-*-*fare
5-*-*-*-*-*cabin
6-*-*-*-*-*-*embarked
5-*-*-*-*-*cabin
3-*-*-*age
4-*-*-*-*sibsp
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
5-*-*-*-*-*parch
6-*-*-*-*-*-*fare
6-*-*-*-*-*-*fare
4-*-*-*-*fare
2-*-*sex
3-*-*-*age
4-*-*-*-*sibsp
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
5-*-*-*-*-*fare
6-*-*-*-*-*-*embarked
6-*-*-*-*-*-*embarked
4-*-*-*-*sibsp
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
5-*-*-*-*-*parch
6-*-*-*-*-*-*fare
7-*-*-*-*-*-*-*embarked
6-*-*-*-*-*-*fare
3-*-*-*age
4-*-*-*-*sibsp
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
5-*-*-*-*-*fare
4-*-*-*-*sibsp
5-*-*-*-*-*parch
6-*-*-*-*-*-*fare
7-*-*-*-*-*-*-*embarked
7-*-*-*-*-*-*-*embarked
6-*-*-*-*-*-*fare
7-*-*-*-*-*-*-*cabin
8-*-*-*-*-*-*-*-*embarked
6-*-*-*-*-*-*fare
5-*-*-*-*-*parch
6-*-*-*-*-*-*fare
6-*-*-*-*-*-*fare
7-*-*-*-*-*-*-*cabin
8-*-*-*-*-*-*-*-*embarked
6-*-*-*-*-*-*fare
5-*-*-*-*-*fare

2.4 在验证集上检验准确率

1
2
3
4
5
6
count = 0
for data in devData:
    if data['survived'] == cartTree.predict(cartTree.root, data):
        count +=1
Accuracy = count/len(devData)
print('验证集准确率：'+ str(Accuracy))

输出结果:

1
验证集准确率：0.78

2.5 进行后剪枝后的准确率

1
2
3
4
5
6
7
cartTree.postPruning(curAccuracy = Accuracy, devData = devData)
count = 0
for data in devData:
    if data['survived'] == cartTree.predict(cartTree.root, data):
        count +=1
Accuracy = count/len(devData)
print('验证集准确率：'+ str(Accuracy))

输出结果（可以看到后剪枝后，验证集上的准确率提升了）：

1
验证集准确率：0.8

2.6 查看剪枝后的决策树

1
cartTree.showTree(cartTree.root, 1)

输出结果（剪枝后，相比于之前的决策树，少了一些分支）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
1-*pclass
2-*-*sex
3-*-*-*age
4-*-*-*-*fare
5-*-*-*-*-*cabin
4-*-*-*-*sibsp
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
6-*-*-*-*-*-*cabin
5-*-*-*-*-*parch
6-*-*-*-*-*-*fare
7-*-*-*-*-*-*-*cabin
6-*-*-*-*-*-*fare
3-*-*-*age
4-*-*-*-*fare
4-*-*-*-*sibsp
5-*-*-*-*-*fare
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
2-*-*sex
3-*-*-*age
4-*-*-*-*fare
5-*-*-*-*-*cabin
4-*-*-*-*fare
5-*-*-*-*-*cabin
6-*-*-*-*-*-*embarked
5-*-*-*-*-*cabin
3-*-*-*age
4-*-*-*-*sibsp
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
5-*-*-*-*-*parch
6-*-*-*-*-*-*fare
6-*-*-*-*-*-*fare
4-*-*-*-*fare
2-*-*sex
3-*-*-*age
4-*-*-*-*sibsp
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
5-*-*-*-*-*fare
6-*-*-*-*-*-*embarked
6-*-*-*-*-*-*embarked
4-*-*-*-*sibsp
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
5-*-*-*-*-*parch
6-*-*-*-*-*-*fare
7-*-*-*-*-*-*-*embarked
6-*-*-*-*-*-*fare
3-*-*-*age
4-*-*-*-*sibsp
5-*-*-*-*-*fare
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
6-*-*-*-*-*-*cabin
7-*-*-*-*-*-*-*embarked
5-*-*-*-*-*fare
4-*-*-*-*sibsp
5-*-*-*-*-*parch
6-*-*-*-*-*-*fare
7-*-*-*-*-*-*-*embarked
7-*-*-*-*-*-*-*embarked
6-*-*-*-*-*-*fare
7-*-*-*-*-*-*-*cabin
8-*-*-*-*-*-*-*-*embarked
6-*-*-*-*-*-*fare
6-*-*-*-*-*-*fare
6-*-*-*-*-*-*fare
7-*-*-*-*-*-*-*cabin
6-*-*-*-*-*-*fare
5-*-*-*-*-*fare

3. 预测测试集

3.1 加载测试集

其实和加载训练数据的函数差不多，但是没有survived特征，并且不需要设置权重w了（因为只需要进行预测）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def loadTestData(filename):
    data = []
    f = list(csv.reader(open(filename, 'r')))[1:]   # 读取去掉表头的部分
    embarkedDist = {'C':1, 'Q':2, 'S':3}    # 无缺失值时，'C':1, 'Q':2, 'S':3
    sibspParch = [1, 2]
    for line in f:
        if int(line[5]) == 0:  # 转化sibsp
            sibsp = 0
        elif int(line[5]) <= 2:
            sibsp = 1
        else:
            sibsp = 2
        
        if int(line[6]) == 0:   # 转化sibsp
            parch = 0
        elif int(line[6]) <= 2:
            parch = 1
        else:
            parch = 2
        dataDist={'pclass': int(line[1]) - 1,
             'sex': 0 if line[3] == 'male' else 1,   # male:0  female:1
             'age': 0 if len(line[4]) == 0 else float(line[4]),   # 有缺失值保存为0
             'sibsp': sibsp,
             'parch': parch,
             'fare': 0 if len(line[8]) == 0 else float(line[8]),  # 测试集中发现有一个缺失值
             'cabin': 0 if len(line[9]) == 0 else 1,   # 有缺失值：0  无缺失值：1
             'embarked': 0 if len(line[10]) == 0 else embarkedDist[line[10]]}   # 有缺失值：0  无缺失值保存为1、2、3
        data.append(dataDist)
    return data
1
2
testData = loadTestData('test.csv')
print(testData[0])

输出结果：

1
{'pclass': 2, 'sex': 0, 'age': 34.5, 'sibsp': 0, 'parch': 0, 'fare': 7.8292, 'cabin': 0, 'embarked': 2}

3.2 进行预测，并将结果写入csv文件

1
2
3
4
5
6
7
8
9
predict = []
for data in testData:
    predict.append(cartTree.predict(cartTree.root, data))
f = open('testPredict.csv','w',encoding='utf-8',newline='' "")
csv_writer = csv.writer(f)
csv_writer.writerow(['PassengerId','Survived'])
for i in range(418):
    csv_writer.writerow([str(i+892),str(predict[i])])
f.close()

3.3 上传kaggle

然后将写好的csv文件上传kaggle即可。

后剪枝处理前：（正确率为0.74401）

UGPP1I.png

后剪枝处理后：（正确率为0.77990，可以看到有明显提升）

UGU8rq.png