k-means算法原理分析与实践

原理分析

一些说明

假定样本集$D=\left\{x_1,x_2,···,x_m\right\}$包含m个无标记样本，每个样本$x_i=(x_{i1},x_{i2},···,x_{in})$是一个n维特征向量，聚类算法将样本集划分为k个不相交的簇$\left\{C_l|l=1,2,3,..,k\right\}$表示，用$\lambda_j\in\left\{ 1,2,…,k \right\}$表示样本$x_j$的簇标记，即$x_j\in C_{\lambda_j}$，所以最终聚类的结果可以用包含m个元素的簇标记向量$\lambda = (\lambda_1,\lambda_2,…,\lambda_j)$表示。

K均值算法

给定样本集$D=\left\{x_1,x_2,···,x_m\right\}$，k均值算法对于一个簇划分$C=\left\{ C_1,C_2,…,C_k \right\}$的最小化平方误差为：

$E=\sum_{i=1}^{k}\sum_{x\in C_i }^{} ||x-\mu_i ||_{2}^{2}$ 其中 $\mu_i = \frac{1}{C_i}\sum_{x\in C_i }^{} x$为簇$C_i$的均值向量。（$||.||_2$为L2范数，Lp范数：向量各个元素绝对值的p次方求和然后求1/p次方）

直观来看的话，$E$就是刻画了簇内样本围绕簇均值向量的紧密程度，$E$值越小，簇内样本相似度就越高，这也就是k均值算法需要达到的最终目的。

下面是k均值算法的伪码表示：

算法实践

使用的是Iris数据集（鸢尾花卉数据集），是一类多重变量分析的数据集。数据集包含150个数据样本，分为3类，每类50个数据，每个数据包含4个属性，分别是花萼长度，花萼宽度，花瓣长度，花瓣宽度。使用k-means聚类算法对数据进行聚类。

需要整个工程文件（包含数据集）可以点击这里

导入python库

版本说明：

• matplotlib:2.2.3
• numpy:1.15.4
• sklearn:0.19.2

import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

加载数据

输入文件名即可，返回一个原始数据的numpy矩阵（维数为150x5，每个增加了一个属性用于存储花的种类）和一个存储颜色的矩阵，用于查看初始数据时画图。

def load_dataset(filename):
    iris_file = open(filename)
    templist = []
    color = []   # 用于给初始数据画图
    while True:
        line = iris_file.readline()
        linelist = line.strip().replace('.','').split(',')   # 将小数点去掉，等效于将数据整体乘以10
        if len(linelist) != 5:
            break
        if linelist[4] == 'Iris-setosa':     # 给花的种类编号  Iris-setosa：0，Iris-versicolor：1，Iris-virginica：2
            classNum = 0
            color.append([1,0,0])    # 红色
        elif linelist[4] == 'Iris-versicolor':
            classNum = 1
            color.append([0,1,0])   # 绿色
        else:
            classNum = 2
            color.append([0,0,1])   # 蓝色
        templist.append([classNum,int(linelist[0]),int(linelist[1]),int(linelist[2]),int(linelist[3])])    #添加到列表
    return np.array(templist),np.array(color)   # 转化为矩阵

iris_data, color = load_dataset('iris.data')

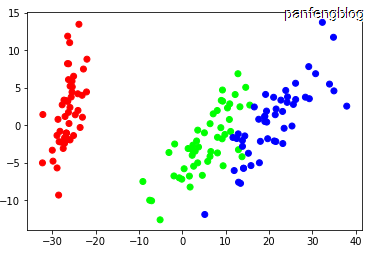
查看初始数据

使用pca将四维数据降至二维，直观查看数据分布：

irisPca = PCA(n_components=2)     # 使用PCA降维便于直观查看初始数据
pcaDate = irisPca.fit_transform(iris_data[:,1:])
X = pcaDate[:,:1].squeeze()
Y = pcaDate[:,1:].squeeze()
print(X.shape, Y.shape, color.shape, X[0], Y[0], color[0])
plt.scatter(X, Y, c=color)
plt.show()

输出结果：

K-means算法

1.随机选取初始向量

这里随机选取了数据的1，2，3个（可随意选取）

u1 = iris_data[0][1:]
u2 = iris_data[1][1:]
u3 = iris_data[2][1:]

2.开始循环

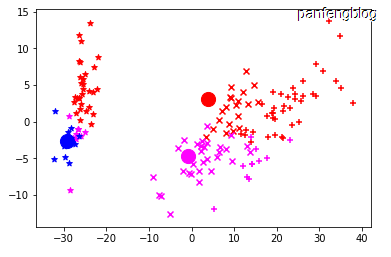
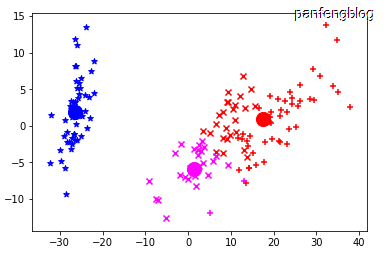
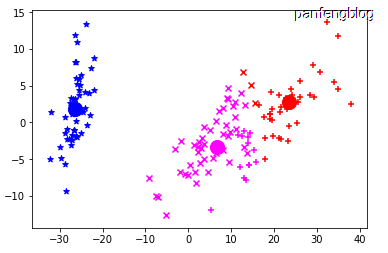
已经选取了初始向量，接下来只需要不断重复：1.将数据根据最近距离划分到相应的簇；2.更新均值向量（在原理分析部分已经说过）。并且在每个循环中，都画出了该轮循环后的一个聚类的状态。（为了能将高维数据直观表示，这里使用了前文训练好的pca降维，不同的颜色代表不同的簇 三种花分别用’*’,’x’和’+’表示，均值向量点用圆点表示）

while True:
    C1 = []   # 三个簇集合
    C2 = []
    C3 = []
    for x in iris_data:
        d1 = np.sum(np.square(x[1:] - u1))   # 求样本与每个初始向量的距离的平方（不需要开方）
        d2 = np.sum(np.square(x[1:] - u2))
        d3 = np.sum(np.square(x[1:] - u3))
        min_d = min(d1, d2, d3)
        if d1 == min_d:   # 根据最小距离分配到相应的簇集合
            C1.append(x)
        elif d2 == min_d:
            C2.append(x)
        else:
            C3.append(x)
    C1 = np.array(C1)
    C2 = np.array(C2)
    C3 = np.array(C3)
    #print(C3.shape)
    u1New = np.array([0,0,0,0]) if C1.shape[0] == 0 else C1[:,1:].sum(axis=0)/C1.shape[0]  # 计算新的均值向量
    u2New = np.array([0,0,0,0]) if C2.shape[0] == 0 else C2[:,1:].sum(axis=0)/C2.shape[0]
    u3New = np.array([0,0,0,0]) if C3.shape[0] == 0 else C3[:,1:].sum(axis=0)/C3.shape[0]
    if all(u1New == u1) and all(u2New == u2) and all(u3New == u3):     # 如果均值向量不再更新，则停止循环
        break
    else:
        u1 = u1New
        u2 = u2New
        u3 = u3New
    
    
    # 下面是画图部分
    # 不同的颜色代表不同的簇
    # 三种花分别用'*','x'和'+'表示
    for x in C1:
        if x[0] == 0:
            [[X,Y]] = irisPca.transform(x[1:].reshape((1,4)))   # 使用之前训练好的pca降维
            plt.scatter(X, Y, c=[1,0,0], marker = '*')
        elif x[0] == 1:
            [[X,Y]] = irisPca.transform(x[1:].reshape((1,4)))
            plt.scatter(X, Y, c=[1,0,0], marker = 'x')
        else:
            [[X,Y]] = irisPca.transform(x[1:].reshape((1,4)))
            plt.scatter(X, Y, c=[1,0,0], marker = '+')
    for x in C2:
        if x[0] == 0:
            [[X,Y]] = irisPca.transform(x[1:].reshape((1,4)))
            plt.scatter(X, Y, c=[1,0,1], marker = '*')
        elif x[0] == 1:
            [[X,Y]] = irisPca.transform(x[1:].reshape((1,4)))
            plt.scatter(X, Y, c=[1,0,1], marker = 'x')
        else:
            [[X,Y]] = irisPca.transform(x[1:].reshape((1,4)))
            plt.scatter(X, Y, c=[1,0,1], marker = '+')
    for x in C3:
        if x[0] == 0:
            [[X,Y]] = irisPca.transform(x[1:].reshape((1,4)))
            plt.scatter(X, Y, c=[0,0,1], marker = '*')
        elif x[0] == 1:
            [[X,Y]] = irisPca.transform(x[1:].reshape((1,4)))
            plt.scatter(X, Y, c=[0,0,1], marker = 'x')
        else:
            [[X,Y]] = irisPca.transform(x[1:].reshape((1,4)))
            plt.scatter(X, Y, c=[0,0,1], marker = '+')
    # 画出均值向量点
    [[X,Y]] = irisPca.transform(u1.reshape((1,4)))
    plt.scatter(X, Y,s=200 , c=[1,0,0], marker = 'o')
    [[X,Y]] = irisPca.transform(u2.reshape((1,4)))
    plt.scatter(X, Y,s=200 , c=[1,0,1], marker = 'o')
    [[X,Y]] = irisPca.transform(u3.reshape((1,4)))
    plt.scatter(X, Y,s=200 , c=[0,0,1], marker = 'o')
    plt.show()

输出结果（这里只截取了一部分输出结果）：

刚开时循环：

循环几轮后：

最终聚类结果：

需要完整代码可以点击这里。